【题目】函数f(x)=Asin(ωx-![]() )+1(A>0, ω>0)与ω=cosωx的部分图象如图所示。
)+1(A>0, ω>0)与ω=cosωx的部分图象如图所示。

(1)求A,a,b的值及函数f(x)的递增区间;
(2)若函数y= g(x-m)(m>![]() )与y= f(x)+ f(x-
)与y= f(x)+ f(x-![]() )的图象的对称轴完全相同,求m的最小值.
)的图象的对称轴完全相同,求m的最小值.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)由题意,得曲线![]() 为
为![]() 的图象,
的图象,![]() 为
为![]() 的图象,求得
的图象,求得![]() 的值,进而求得函数
的值,进而求得函数![]() 的解析式,即求解
的解析式,即求解![]() 的单调区间;
的单调区间;
(2)由(1)得![]() 的解析式,根据图象的对称轴相同,得到
的解析式,根据图象的对称轴相同,得到![]() ,即可得到实数
,即可得到实数![]() 的最小值.
的最小值.
试题解析:
(1)由图可知,曲线C1为的图象,C2为f(x)的图象,
则A=3-1=2,![]() T=
T=![]() ,∴T=
,∴T=![]() =
=![]() ,
,![]() =2.
=2.
∴f (x)=2sin(2x-![]() )+1,令2x-
)+1,令2x-![]() =
=![]() 得x=
得x=![]() ,∴a=
,∴a=![]() ,b=a+
,b=a+![]() =
=![]()
令-![]() +2k
+2k![]() ≤2x-
≤2x-![]() ≤
≤![]() +2k
+2k![]() ,
,![]() ,解得-
,解得-![]() +k
+k![]() ≤x≤
≤x≤![]() +k
+k![]() ,
,
故f(x)的递增区间为[k![]() +
+![]() ]
]![]()
(2)∵g(x)=cos2x,∴g(x-m)=cos(2x-2m),
f(x)+ f(x-![]() )=2+2sin(2x-
)=2+2sin(2x-![]() )-2cos(2x-
)-2cos(2x-![]() )=2+2
)=2+2![]() (2x-
(2x-![]() -
-![]() )
)
=2+2![]() (2x-
(2x-![]() )
)
令2x-2m=k![]() 得y=g(x-m)的图象的对称轴方程为x=m+
得y=g(x-m)的图象的对称轴方程为x=m+![]()
令2x-![]() =
=![]() +k
+k![]() 得y= f(x)+ f(x-
得y= f(x)+ f(x-![]() )的图象的对称轴方程为
)的图象的对称轴方程为
x =![]() +
+![]() ∴m=
∴m=![]() +
+![]()
∴m>![]() , ∴m的最小值为
, ∴m的最小值为![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】
 年
年 月
月 日,“国际教育信息化大会”在山东青岛开幕.为了解哪些人更关注“国际教育信息化大会”,某机构随机抽取了年龄在
日,“国际教育信息化大会”在山东青岛开幕.为了解哪些人更关注“国际教育信息化大会”,某机构随机抽取了年龄在 -
- 岁之间的
岁之间的 人进行调查,并按年龄绘制成频率分布直方图,如图所示,其分组区间为:
人进行调查,并按年龄绘制成频率分布直方图,如图所示,其分组区间为: ,
, ,
, ,
, ,
, ,
, .把年龄落在区间
.把年龄落在区间 和
和 内的人分别称为“青少年”和“中老年”.
内的人分别称为“青少年”和“中老年”.
关注
不关注
合计
青少年

中老年
合计



(1)根据频率分布直方图求样本的中位数(保留两位小数)和众数;
(2)根据已知条件完成
 列联表,并判断能否有
列联表,并判断能否有 的把握认为“中老年”比“青少年”更加关注“国际教育信息化大会”;
的把握认为“中老年”比“青少年”更加关注“国际教育信息化大会”; -
科目: 来源: 题型:
查看答案和解析>>【题目】设等差数列{an}的前n项和为Sn , 且满足S17>0,S18<0,则
 ,
,  ,…,
,…,  中最大的项为( )
中最大的项为( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
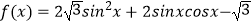
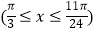 .
.
(1)求函数f(x)的值域;
(2)已知锐角△ABC的两边长分别为函数f(x)的最大值与最小值,且△ABC的外接圆半径为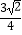 ,求△ABC的面积.
,求△ABC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知经过原点的直线与椭圆
 交于
交于 两点,点
两点,点 为椭圆上不同于
为椭圆上不同于 的一点,直线
的一点,直线 的斜率均存在,且直线
的斜率均存在,且直线 的斜率之积为
的斜率之积为 .
.(1)求椭圆
 的离心率;
的离心率;(2)若
 ,设
,设 分别为椭圆的左、右焦点,斜率为
分别为椭圆的左、右焦点,斜率为 的直线
的直线 经过椭圆的右焦点,且与椭圆交于
经过椭圆的右焦点,且与椭圆交于 两点,若点
两点,若点 在以
在以 为直径的圆内部,求
为直径的圆内部,求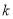 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,某班一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,其中,频率分布直方图的分组区间分别为[50,60),[60,70),[70,80),[80,90),[90,100],据此解答如下问题.
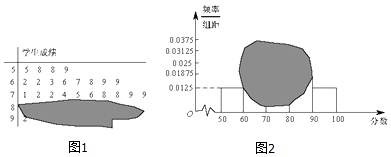
(Ⅰ)求全班人数及分数在[80,100]之间的频率;
(Ⅱ)现从分数在[80,100]之间的试卷中任取 3 份分析学生情况,设抽取的试卷分数在[90,100]的份数为X,求X的分布列和数学望期. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
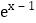 +ax,aR,
+ax,aR,(1)讨论函数f(x)的单调区间;
(2)求证:
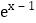 ≥x;
≥x;(3)求证:当a≥-2时,x[1,+ ∞),f(x)+lnx≥a+1恒成立.
相关试题

