【题目】已知函数f(x)=2sinωxcosωx+2![]() sin2ωx﹣
sin2ωx﹣![]() (ω>0)的最小正周期为π.
(ω>0)的最小正周期为π.
(1)求函数f(x)的单调增区间;
(2)将函数f(x)的图象向左平移![]() 个单位,再向上平移1个单位,得到函数y=g(x)的图象,若y=g(x)在[0,b](b>0)上至少含有10个零点,求b的最小值.
个单位,再向上平移1个单位,得到函数y=g(x)的图象,若y=g(x)在[0,b](b>0)上至少含有10个零点,求b的最小值.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)第一步根据降幂公式![]() ,
,![]() 化简,第二步,对降幂后的式子,再根据辅助角公式化简,得到
化简,第二步,对降幂后的式子,再根据辅助角公式化简,得到![]() ,令
,令![]() ,
,![]() 得到函数的单调递增区间;(2)根据三角函数的图像变换规律,“左+右-,上+下-”,得到函数
得到函数的单调递增区间;(2)根据三角函数的图像变换规律,“左+右-,上+下-”,得到函数![]() ,令
,令![]() ,得到
,得到![]() 的值,根据
的值,根据![]() 的取值集合,
的取值集合,![]() 只需大于等于 10个点的横坐标即可.
只需大于等于 10个点的横坐标即可.
试题解析:(1)由题意得f(x)=2sinωxcosωx+2![]() sin2ωx﹣
sin2ωx﹣![]() =sin2ωx﹣
=sin2ωx﹣![]() cos2ωx=2sin(2ωx﹣
cos2ωx=2sin(2ωx﹣![]() ),由最小正周期为π,得ω=1,
),由最小正周期为π,得ω=1,
所以![]() ,
,
由![]() ,整理得
,整理得![]()
![]() ,
,
所以函数f(x)的单调增区间是![]() .
.
(2)将函数f(x)的图象向左平移![]() 个单位,再向上平移1个单位,得到y=2sin2x+1的图象,所以g(x)=2sin2x+1,
个单位,再向上平移1个单位,得到y=2sin2x+1的图象,所以g(x)=2sin2x+1,
令g(x)=0,得![]() 或
或![]() ,
,
所以在[0,π]上恰好有两个零点,若y=g(x)在[0,b]上有10个零点,
则b不小于第10个零点的横坐标即可,即b的最小值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校为加强学生的交通安全教育,对学校旁边
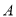 ,
,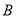 两个路口进行了8天的检测调查,得到每天各路口不按交通规则过马路的学生人数(如茎叶图所示),且
两个路口进行了8天的检测调查,得到每天各路口不按交通规则过马路的学生人数(如茎叶图所示),且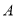 路口数据的平均数比
路口数据的平均数比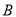 路口数据的平均数小2.
路口数据的平均数小2.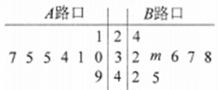
(1)求出
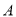 路口8个数据中的中位数和茎叶图中
路口8个数据中的中位数和茎叶图中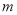 的值;
的值;(2)在
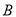 路口的数据中任取大于35的2个数据,求所抽取的两个数据中至少有一个不小于40的概率.
路口的数据中任取大于35的2个数据,求所抽取的两个数据中至少有一个不小于40的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是正方形,延长CD至E,使得DE=CD.若动点P从点A出发,沿正方形的边按逆时针方向运动一周回到A点,其
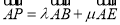 下列叙述正确的是( )
下列叙述正确的是( )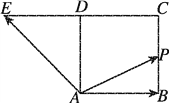
A. 满足λ+μ=2的点P必为BC的中点
B. 满足λ+μ=1的点P有且只有一个
C. λ+μ的最大值为3
D. λ+μ的最小值不存在
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C:
 +
+ =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,椭圆C的长轴长为4.
,椭圆C的长轴长为4.(1)求椭圆C的方程;
(2)已知直线l:y=kx+
 与椭圆C交于A,B两点,是否存在实数k使得以线段AB为直径的圆恰好经过坐标原点O?若存在,求出k的值;若不存在,请说明理由.
与椭圆C交于A,B两点,是否存在实数k使得以线段AB为直径的圆恰好经过坐标原点O?若存在,求出k的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量a=(cosx,sinx),b=(-cosx,cosx),c=(-1,0).
(1)若x=
 ,求向量a,c的夹角;
,求向量a,c的夹角;(2)当x∈
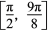 时,求函数f(x)=2a·b+1的值域.
时,求函数f(x)=2a·b+1的值域. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=2sinxcosx-
 cos2x.
cos2x.(1)求f(0)的值及函数f(x)的单调递增区间;
(2)求函数f(x)在区间
 上的最大值和最小值.
上的最大值和最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】命题p:关于x的方程x2+ax+2=0无实根,命题q:函数f(x)=logax在(0,+∞)上单调递增,若“p∧q”为假命题,“p∨q”真命题,求实数a的取值范围
相关试题

