【题目】某学校为加强学生的交通安全教育,对学校旁边![]() ,
,![]() 两个路口进行了8天的检测调查,得到每天各路口不按交通规则过马路的学生人数(如茎叶图所示),且
两个路口进行了8天的检测调查,得到每天各路口不按交通规则过马路的学生人数(如茎叶图所示),且![]() 路口数据的平均数比
路口数据的平均数比![]() 路口数据的平均数小2.
路口数据的平均数小2.
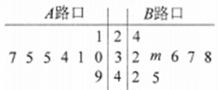
(1)求出![]() 路口8个数据中的中位数和茎叶图中
路口8个数据中的中位数和茎叶图中![]() 的值;
的值;
(2)在![]() 路口的数据中任取大于35的2个数据,求所抽取的两个数据中至少有一个不小于40的概率.
路口的数据中任取大于35的2个数据,求所抽取的两个数据中至少有一个不小于40的概率.
参考答案:
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)由茎叶图可得![]() 路口
路口![]() 个数据中
个数据中![]() 为最中间两个数,由此计算中位数,又
为最中间两个数,由此计算中位数,又![]() 路口
路口![]() 个数据的平均数为
个数据的平均数为![]() ,可得
,可得![]() ;(2)
;(2)![]() 在路口的数据中任取
在路口的数据中任取![]() 个大于
个大于![]() 的数据,有
的数据,有![]() 种可能,其中“至少有一次抽取的数据不小于
种可能,其中“至少有一次抽取的数据不小于![]() ”的情况有
”的情况有![]() 种,故所求概率为
种,故所求概率为![]() .
.
试题解析:(1)![]() 路口8个数据的中位数为
路口8个数据的中位数为![]() .
.
∵![]() 路口8个数据的平均数为
路口8个数据的平均数为![]() ,
,
∴![]() 路口8个数据的平均数为36,
路口8个数据的平均数为36,
∴![]() ,
,![]() .
.
(2)![]() 在路口的数据中任取2个大于35的数据,有如下10种可能结果:
在路口的数据中任取2个大于35的数据,有如下10种可能结果:
(36,37),(36,38),(36,42),(36,45),(37,38),(37,42),(37,45),
(38,42),(38,45),(42,45).
其中“至少有一次抽取的数据不小于40”的情况有如下7种:
(36,42),(36,45),(37,42),(37,45),(38,42),(38,45),(42,45).
故所求的概率为![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某企业的两座建筑物AB,CD的高度分别为20m和40m,其底部BD之间距离为20m.为响应创建文明城市号召,进行亮化改造,现欲在建筑物AB的顶部A处安装一投影设备,投影到建筑物CD上形成投影幕墙,既达到亮化目的又可以进行广告宣传.已知投影设备的投影张角∠EAF为
 ,投影幕墙的高度EF越小,投影的图像越清晰.设投影光线的上边沿AE与水平线AG所成角为α,幕墙的高度EF为y(m).
,投影幕墙的高度EF越小,投影的图像越清晰.设投影光线的上边沿AE与水平线AG所成角为α,幕墙的高度EF为y(m).(1)求y关于α的函数关系式
 ,并求出定义域;
,并求出定义域;(2)当投影的图像最清晰时,求幕墙EF的高度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某同学用“五点法”画函数f(x)=Asin(ωx+φ)(ω>0,|φ|<
 )在某一个周期内的图象时,列表并填入了部分数据,如下表:
)在某一个周期内的图象时,列表并填入了部分数据,如下表:ωx+φ
0

π

2π
x


Asin(ωx+φ)
0
3
0
-3
0
(1)请将上表数据补充完整,填写在答题卡上相应位置,并直接写出函数f(x)的解析式;
(2)令g(x)=f (x+
 )-
)- ,当x∈[
,当x∈[ ,
,  ]时,恒有不等式g(x)-a-3<0成立,求实数a的取值范围
]时,恒有不等式g(x)-a-3<0成立,求实数a的取值范围 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中错误的是_______(填序号)
①命题“
 有
有 ”的否定是“
”的否定是“ 有
有 ”;
”;②若一个命题的逆命题为真命题,则它的否命题也一定为真命题;
③已知
 ,
,  ,若命题
,若命题 为真命题,则
为真命题,则 的取值范围是
的取值范围是 ;
;④“
 ”是“
”是“ ”成立的充分条件.
”成立的充分条件. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是正方形,延长CD至E,使得DE=CD.若动点P从点A出发,沿正方形的边按逆时针方向运动一周回到A点,其
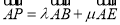 下列叙述正确的是( )
下列叙述正确的是( )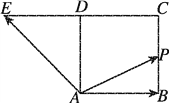
A. 满足λ+μ=2的点P必为BC的中点
B. 满足λ+μ=1的点P有且只有一个
C. λ+μ的最大值为3
D. λ+μ的最小值不存在
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C:
 +
+ =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,椭圆C的长轴长为4.
,椭圆C的长轴长为4.(1)求椭圆C的方程;
(2)已知直线l:y=kx+
 与椭圆C交于A,B两点,是否存在实数k使得以线段AB为直径的圆恰好经过坐标原点O?若存在,求出k的值;若不存在,请说明理由.
与椭圆C交于A,B两点,是否存在实数k使得以线段AB为直径的圆恰好经过坐标原点O?若存在,求出k的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=2sinωxcosωx+2
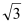 sin2ωx﹣
sin2ωx﹣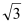 (ω>0)的最小正周期为π.
(ω>0)的最小正周期为π.(1)求函数f(x)的单调增区间;
(2)将函数f(x)的图象向左平移
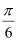 个单位,再向上平移1个单位,得到函数y=g(x)的图象,若y=g(x)在[0,b](b>0)上至少含有10个零点,求b的最小值.
个单位,再向上平移1个单位,得到函数y=g(x)的图象,若y=g(x)在[0,b](b>0)上至少含有10个零点,求b的最小值.
相关试题

