搜索
【题目】已知正三棱柱
的正（主）视图和侧（左）视图如图所示,设
,
的中心分别为
, 
,现将此三棱柱绕直线
旋转,射线
旋转所成角为
弧度（
可以取到任意一个实数）,对应的俯视图的面积为
,则函数
的最大值为__________,最小正周期为__________.
参考答案：
【答案】 8 
【解析】由题意可知，正三棱柱的底面三角形的高为
，正三角形的边长为2，
俯视图是矩形，当此三棱柱绕直线OO′旋转，在旋转过程中对应的俯视图，底面正三角形的边在俯视图中为矩形的边长时，俯视图的面积最大，令俯视图的面积为S，则S的最大值为：2×4=8.
因为正三角形的内角均为
，所以函数S(x)的最小正周期为
.
点睛:思考三视图还原空间几何体首先应深刻理解三视图之间的关系，遵循“长对正，高平齐，宽相等”的基本原则，其内涵为正视图的高是几何体的高，长是几何体的长；俯视图的长是几何体的长，宽是几何体的宽；侧视图的高是几何体的高，宽是几何体的宽.由三视图画出直观图的步骤和思考方法：1、首先看俯视图，根据俯视图画出几何体地面的直观图；2、观察正视图和侧视图找到几何体前、后、左、右的高度；3、画出整体，然后再根据三视图进行调整.
-
科目： 来源： 题型：
查看答案和解析>>【题目】.如图，已知
，图中的一系列圆是圆心分别为A、B的两组同心圆，每组同心圆的半径分别是1，2，3，…，n，….利用这两组同心圆可以画出以A、B为焦点的双曲线. 若其中经过点M、N、P的双曲线的离心率分别是
.则它们的大小关系是 （用“
”连接）. 
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在四棱锥P﹣ABCD中，PA⊥平面ABCD，PA=AB=AD=2，四边形ABCD满足AB⊥AD，BC∥AD且BC=4，点M为PC的中点，点E为BC边上的点，且
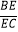=λ．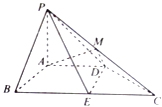 
（1）求证：平面ADM⊥平面PBC；
（2）是否存在实数λ，使得二面角P﹣DE﹣B的余弦值为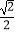
？若存在，求出实数λ的值，若不存在，请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知椭圆C的焦点坐标是F1（﹣1，0）、F2（1，0），过点F2垂直于长轴的直线l交椭圆C于B、D两点，且|BD|=3．
（1）求椭圆C的方程；
（2）过定点P（0，2）且斜率为k的直线l与椭圆C相交于不同两点M，N，试判断：在x轴上是否存在点A（m，0），使得以AM，AN为邻边的平行四边形为菱形？若存在，求出实数m的取值范围，若不存在，请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】定义在（0，+∞）的函数f（x）满足如下三个条件：
①对于任意正实数a、b，都有f（ab）=f（a）+f（b）-1；
②f（2）=0；
③x＞1时，总有f（x）＜1．
（1）求f（1）及
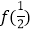的值；（2）求证：函数f（x）在（0，+∞）上是减函数；
（3）如果存在正数k，使关于x的方程f（kx）+f（2-x）=-1有解，求正实数k的取值范围．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在底面是正方形的四棱锥
中, 
, 
,点
在
上,且
.
（Ⅰ）求证:
平面
;（Ⅱ）求二面角
的余弦值. -
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数
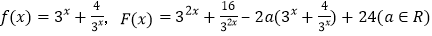．（1）若函数
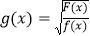的值域为[0，+∞），求实数a的取值范围；（2）若关于x的不等式F（x）＞af（x）+12恒成立，求实数a的取值范围．
相关试题
