【题目】已知函数![]() .
.
(1)若函数![]() 的值域为[0,+∞),求实数a的取值范围;
的值域为[0,+∞),求实数a的取值范围;
(2)若关于x的不等式F(x)>af(x)+12恒成立,求实数a的取值范围.
参考答案:
【答案】(1)4;(2)(-∞,![]() ).
).
【解析】
(1)换元令f(x)=t后,求出g(x)![]() 的值域后,与已知值域比较得:8﹣2a=0,得a=4;
的值域后,与已知值域比较得:8﹣2a=0,得a=4;
(2)换元令f(x)=t后,转化为关于t的不等式在[4,+∞)上恒成立.
解:(1)令![]() . 由对勾函数的性质可知:y=t+
. 由对勾函数的性质可知:y=t+![]() 在[4,+∞)上递增,
在[4,+∞)上递增,
∴g(x)=![]() =
=![]() ≥
≥![]() =
=![]()
依题意:8-2a=0,∴a=4
(2)令f(x)=t,
则不等式转化为:t2-2at+16>at+12,即3a<t+![]() ,对任意t∈[4,+∞)恒成立,
,对任意t∈[4,+∞)恒成立,
由对勾函数的性质可知:y=t+![]() 在[4,+∞)上递增,所以t=4时,y取最小值8,
在[4,+∞)上递增,所以t=4时,y取最小值8,
所以3a<8,∴a![]()
所以实数a的实数的取值范围为(-∞,![]() )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正三棱柱
 的正(主)视图和侧(左)视图如图所示,设
的正(主)视图和侧(左)视图如图所示,设 ,
, 的中心分别为
的中心分别为 ,
,  ,现将此三棱柱绕直线
,现将此三棱柱绕直线 旋转,射线
旋转,射线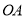 旋转所成角为
旋转所成角为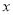 弧度(
弧度(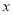 可以取到任意一个实数),对应的俯视图的面积为
可以取到任意一个实数),对应的俯视图的面积为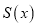 ,则函数
,则函数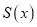 的最大值为__________,最小正周期为__________.
的最大值为__________,最小正周期为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义在(0,+∞)的函数f(x)满足如下三个条件:
①对于任意正实数a、b,都有f(ab)=f(a)+f(b)-1;
②f(2)=0;
③x>1时,总有f(x)<1.
(1)求f(1)及
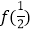 的值;
的值;(2)求证:函数f(x)在(0,+∞)上是减函数;
(3)如果存在正数k,使关于x的方程f(kx)+f(2-x)=-1有解,求正实数k的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在底面是正方形的四棱锥
 中,
中,  ,
,  ,点
,点 在
在 上,且
上,且 .
.
(Ⅰ)求证:
 平面
平面 ;
;(Ⅱ)求二面角
 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=ex﹣ax﹣1(a为常数),曲线y=f(x)在与y轴的交点A处的切线斜率为﹣1.
(1)求a的值及函数y=f(x)的单调区间;
(2)若x1<ln2,x2>ln2,且f(x1)=f(x2),证明:x1+x2<2ln2. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在棱长为
 的正方体
的正方体 中,点
中,点 、
、 是棱
是棱 、
、 的中点,
的中点,  是底面
是底面 上(含边界)一动点,满足
上(含边界)一动点,满足 ,则线段
,则线段 长度的取值范围是( )
长度的取值范围是( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 为奇函数.
为奇函数.(1)求
 的值;
的值;(2)求函数
 在
在 的最小值;
的最小值;(3)若函数
 在区间
在区间 上单调递减,求实数
上单调递减,求实数 的取值范围.
的取值范围.
相关试题

