【题目】定义在(0,+∞)的函数f(x)满足如下三个条件:
①对于任意正实数a、b,都有f(ab)=f(a)+f(b)-1;
②f(2)=0;
③x>1时,总有f(x)<1.
(1)求f(1)及![]() 的值;
的值;
(2)求证:函数f(x)在(0,+∞)上是减函数;
(3)如果存在正数k,使关于x的方程f(kx)+f(2-x)=-1有解,求正实数k的取值范围.
参考答案:
【答案】(1)f(1)=1;f(![]() )=2;(2)详见解析;(3)[8,+∞).
)=2;(2)详见解析;(3)[8,+∞).
【解析】
(1)令a=b=1,a=2,b![]() ,即可求得f(1)及
,即可求得f(1)及![]() 的值;
的值;
(2)当x>1时,f(x)<1,根据函数单调性的定义讨论函数的单调性;
(3)把f(kx)+f(2﹣x)根据条件转化为f[kx(2﹣x)]﹣1,根据函数的单调性把函数值转化为自变量x的方程,分离参数转化我求函数的值域即可得到所求范围.
解:(1)令a=b=1得f(1)=2f(1)-1,
即有f(1)=1;
令a=2,b=![]() ,可得f(1)=f(2)+f(
,可得f(1)=f(2)+f(![]() )-1=f(
)-1=f(![]() )-1=1,
)-1=1,
即有f(![]() )=2;
)=2;
(2)证明:设0<x1<x2,可得![]() >1,
>1,
可得f(![]() )<1,
)<1,
由f(x2)=f(x1![]() )=f(x1)+f(
)=f(x1)+f(![]() )-1<f(x1),
)-1<f(x1),
可得函数f(x)在(0,+∞)上是减函数;
(3)由f(4)=2f(2)-1=-1,
f(8)=f(2)+f(4)-1=-2,
可得关于x的方程f(kx)+f(2-x)=-1即为f(kx(2-x))=-2=f(8),
函数f(x)在(0,+∞)上是减函数,
可得kx(2-x)=8在0<x<2有解,
即有k=![]() ,
,
由0<x<2可得x(2-x)∈(0,1],
则k的范围是[8,+∞).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,PA=AB=AD=2,四边形ABCD满足AB⊥AD,BC∥AD且BC=4,点M为PC的中点,点E为BC边上的点,且
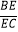 =λ.
=λ. 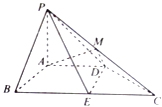
(1)求证:平面ADM⊥平面PBC;
(2)是否存在实数λ,使得二面角P﹣DE﹣B的余弦值为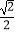 ?若存在,求出实数λ的值,若不存在,请说明理由.
?若存在,求出实数λ的值,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C的焦点坐标是F1(﹣1,0)、F2(1,0),过点F2垂直于长轴的直线l交椭圆C于B、D两点,且|BD|=3.
(1)求椭圆C的方程;
(2)过定点P(0,2)且斜率为k的直线l与椭圆C相交于不同两点M,N,试判断:在x轴上是否存在点A(m,0),使得以AM,AN为邻边的平行四边形为菱形?若存在,求出实数m的取值范围,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知正三棱柱
 的正(主)视图和侧(左)视图如图所示,设
的正(主)视图和侧(左)视图如图所示,设 ,
, 的中心分别为
的中心分别为 ,
,  ,现将此三棱柱绕直线
,现将此三棱柱绕直线 旋转,射线
旋转,射线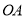 旋转所成角为
旋转所成角为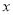 弧度(
弧度(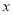 可以取到任意一个实数),对应的俯视图的面积为
可以取到任意一个实数),对应的俯视图的面积为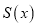 ,则函数
,则函数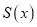 的最大值为__________,最小正周期为__________.
的最大值为__________,最小正周期为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在底面是正方形的四棱锥
 中,
中,  ,
,  ,点
,点 在
在 上,且
上,且 .
.
(Ⅰ)求证:
 平面
平面 ;
;(Ⅱ)求二面角
 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
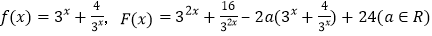 .
.(1)若函数
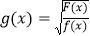 的值域为[0,+∞),求实数a的取值范围;
的值域为[0,+∞),求实数a的取值范围;(2)若关于x的不等式F(x)>af(x)+12恒成立,求实数a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=ex﹣ax﹣1(a为常数),曲线y=f(x)在与y轴的交点A处的切线斜率为﹣1.
(1)求a的值及函数y=f(x)的单调区间;
(2)若x1<ln2,x2>ln2,且f(x1)=f(x2),证明:x1+x2<2ln2.
相关试题

