【题目】已知椭圆![]() :
: ![]() 的长轴长为
的长轴长为![]() ,且椭圆
,且椭圆![]() 与圆
与圆![]() :
: ![]() 的公共弦长为
的公共弦长为![]() .
.
(1)求椭圆![]() 的方程.
的方程.
(2)经过原点作直线![]() (不与坐标轴重合)交椭圆于
(不与坐标轴重合)交椭圆于![]() ,
, ![]() 两点,
两点, ![]() 轴于点
轴于点![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,且
上,且![]() ,求证:
,求证: ![]() ,
, ![]() ,
, ![]() 三点共线..
三点共线..
参考答案:
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】试题分析:(1)根据题意列出关于![]() 、
、![]() 、
、![]() 的方程组,结合性质
的方程组,结合性质![]() , ,求出
, ,求出![]() 、
、![]() 、
、![]() ,即可得结果;(2)设
,即可得结果;(2)设![]() ,
, ![]() ,则
,则![]() ,
, ![]() .
.
因为点![]() ,
, ![]() 都在椭圆
都在椭圆![]() 上,所以
上,所以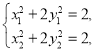 ,利用“点差法”证明
,利用“点差法”证明![]()
![]() ,即可得结论.
,即可得结论.
试题解析:(1)由题意得![]() ,则
,则![]() .
.
由椭圆![]() 与圆
与圆![]() :
: ![]() 的公共弦长为
的公共弦长为![]() ,
,
其长度等于圆![]() 的直径,
的直径,
可得椭圆![]() 经过点
经过点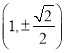 ,
,
所以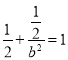 ,解得
,解得![]() .
.
所以椭圆![]() 的方程为
的方程为![]() .
.
(2)证明:设![]() ,
, ![]() ,则
,则![]() ,
, ![]() .
.
因为点![]() ,
, ![]() 都在椭圆
都在椭圆![]() 上,所以
上,所以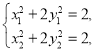
所以![]()
![]() ,
,
即![]() .
.
又![]()
![]() ,
,
所以![]() ,
,
即![]() ,
,
所以![]()
所以![]()
又![]()
![]() ,
,
所以![]() ,
,
所以![]() ,
, ![]() ,
, ![]() 三点共线.
三点共线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=4x+a2x+3,a∈R.
(1)当a=﹣4时,且x∈[0,2],求函数f(x)的值域;
(2)若关于x的方程f(x)=0在(0,+∞)上有两个不同实根,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四棱锥S﹣ABCD,底面ABCD为菱形,SA⊥平面ABCD,∠ADC=60°,E,F分别是SC,BC的中点.
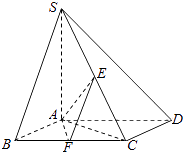
(1)证明:SD⊥AF;
(2)若AB=2,SA=4,求二面角F﹣AE﹣C的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
,  (
( ,
,  为自然对数的底数).
为自然对数的底数).(1)试讨论函数
 的极值情况;
的极值情况;(2)证明:当
 且
且 时,总有
时,总有 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
 在以
在以 为直径的圆
为直径的圆 上,
上,  垂直与圆
垂直与圆 所在平面,
所在平面,  为
为 的垂心.
的垂心.(1)求证:平面
 平面
平面 ;
;(2)若
 ,点
,点 在线段
在线段 上,且
上,且 ,求三棱锥
,求三棱锥 的体积.
的体积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
 =(cos
=(cos  x,sin
x,sin  x),
x),  =(cos
=(cos  x,﹣sin
x,﹣sin  x),且x∈[0,
x),且x∈[0,  ].求:
].求:
(1) 及
及  ;
;
(2)若f(x)= ﹣2λ
﹣2λ  的最小值是﹣
的最小值是﹣  ,求λ的值.
,求λ的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】商品在近30天内每件的销售价格P(元)与时间t(天)的函数关系p=
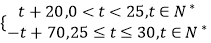
该商品的日销售量Q(件)时间t(天)的函数关系Q=﹣t+40(0<t≤30,t∈N*)
求该商品的日销售额的最大值,并指出日销售额最大一天是30天中的第几天?
相关试题

