【题目】已知向量 ![]() =(cos
=(cos ![]() x,sin
x,sin ![]() x),
x), ![]() =(cos
=(cos ![]() x,﹣sin
x,﹣sin ![]() x),且x∈[0,
x),且x∈[0, ![]() ].求:
].求:
(1)![]() 及
及 ![]() ;
;
(2)若f(x)= ![]() ﹣2λ
﹣2λ ![]() 的最小值是﹣
的最小值是﹣ ![]() ,求λ的值.
,求λ的值.
参考答案:
【答案】
(1)解: ![]() =cos2x
=cos2x
![]() =
= ![]()
∵x∈[0, ![]() ],∴cosx>0,∴
],∴cosx>0,∴ ![]() =2cosx.
=2cosx.
(2)解:f(x)=cos2x﹣4λcosx=2cos2x﹣1﹣4λcosx,设t=cosx,
则∵ ![]() ,∴t∈[0,1]
,∴t∈[0,1]
即y=f(x)=2t2﹣4λt﹣1=2(t﹣λ)2﹣1﹣2λ2.
①λ<0时,当且仅当t=0时,y取最小值﹣1,这与已知矛盾
②当0≤λ≤1时,当且仅当t=λ时,y取得最小值﹣1﹣2λ2,
由已知得 ![]() ,解得λ=
,解得λ= ![]()
③当λ>1时,当且仅当t=1时,y取得最小值1﹣4λ.
由已知得 ![]() ,解得λ=
,解得λ= ![]() ,这与λ>1相矛盾.
,这与λ>1相矛盾.
综上λ= ![]() 为所求.
为所求.
【解析】(1)利用向量的数量积公式,结合差角的三角函数,角的范围,即可得出结论;(2)f(x)=cos2x﹣4λcosx=2cos2x﹣1﹣4λcosx,设t=cosx,可得y=f(x)=2t2﹣4λt﹣1=2(t﹣λ)2﹣1﹣2λ2 , 分类讨论,利用最小值是﹣ ![]() ,即可求λ的值.
,即可求λ的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
,  (
( ,
,  为自然对数的底数).
为自然对数的底数).(1)试讨论函数
 的极值情况;
的极值情况;(2)证明:当
 且
且 时,总有
时,总有 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 :
:  的长轴长为
的长轴长为 ,且椭圆
,且椭圆 与圆
与圆 :
:  的公共弦长为
的公共弦长为 .
.(1)求椭圆
 的方程.
的方程.(2)经过原点作直线
 (不与坐标轴重合)交椭圆于
(不与坐标轴重合)交椭圆于 ,
,  两点,
两点,  轴于点
轴于点 ,点
,点 在椭圆
在椭圆 上,且
上,且 ,求证:
,求证:  ,
,  ,
,  三点共线..
三点共线.. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
 在以
在以 为直径的圆
为直径的圆 上,
上,  垂直与圆
垂直与圆 所在平面,
所在平面,  为
为 的垂心.
的垂心.(1)求证:平面
 平面
平面 ;
;(2)若
 ,点
,点 在线段
在线段 上,且
上,且 ,求三棱锥
,求三棱锥 的体积.
的体积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】商品在近30天内每件的销售价格P(元)与时间t(天)的函数关系p=
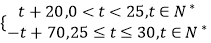
该商品的日销售量Q(件)时间t(天)的函数关系Q=﹣t+40(0<t≤30,t∈N*)
求该商品的日销售额的最大值,并指出日销售额最大一天是30天中的第几天? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C:
 (a>b>0)的离心率为
(a>b>0)的离心率为  ,左焦点为F(﹣1,0),过点D(0,2)且斜率为k的直线l交椭圆于A,B两点.
,左焦点为F(﹣1,0),过点D(0,2)且斜率为k的直线l交椭圆于A,B两点.
(1)求椭圆C的标准方程;
(2)求k的取值范围;
(3)在y轴上,是否存在定点E,使
 恒为定值?若存在,求出E点的坐标和这个定值;若不存在,说明理由.
恒为定值?若存在,求出E点的坐标和这个定值;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 (
( ),数列
),数列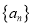 的前
的前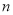 项和为
项和为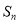 ,点
,点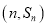 在
在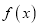 图象上,且
图象上,且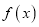 的最小值为
的最小值为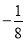 .
.(1)求数列
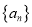 的通项公式;
的通项公式;(2)数列
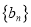 满足
满足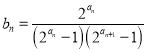 ,记数列
,记数列 的前
的前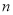 项和为
项和为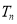 ,求证:
,求证: 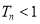 .
.
相关试题

