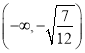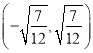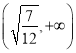【题目】已知函数![]() ,
, ![]() .
.
(Ⅰ)当![]() 时,求证:过点
时,求证:过点![]() 有三条直线与曲线
有三条直线与曲线![]() 相切;
相切;
(Ⅱ)当![]() 时,
时, ![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(I)详见解析;(II)![]() .
.
【解析】试题分析:
(1)首先对函数求导,写出切线方程,讨论方程根的分布可得过点![]() 有三条直线与曲线
有三条直线与曲线![]() 相切;
相切;
(2)利用题意构造函数![]() ,由新函数的性质可得实数
,由新函数的性质可得实数![]() 的取值范围是
的取值范围是![]() .
.
试题解析:解法一:(Ⅰ)当![]() 时,
时, ![]() ,
,
![]()
![]()
设直线与曲线![]() 相切,其切点为
相切,其切点为![]() ,
,
则曲线![]() 在点
在点![]() 处的切线方程为:
处的切线方程为: ![]() ,
,
因为切线过点![]() ,所以
,所以![]() ,
,
即![]()
![]() ,
,
∵![]() ,∴
,∴![]() ,
,
设![]() ,
,
∵![]() ,
, ![]() ,
, ![]() ,
, ![]()
∴![]() 在三个区间
在三个区间![]() 上至少各有一个根
上至少各有一个根
又因为一元三次方程至多有三个根,所以方程![]() 恰有三个根,
恰有三个根,
故过点![]() 有三条直线与曲线
有三条直线与曲线![]() 相切.
相切.
(Ⅱ)∵当![]() 时,
时, ![]() ,即当
,即当![]() 时,
时, ![]()
∴当![]() 时,
时, ![]() ,
,
设![]() ,则
,则![]() ,
,
设![]() ,则
,则![]() .
.
(1)当![]() 时,∵
时,∵![]() ,∴
,∴![]() ,从而
,从而![]() (当且仅当
(当且仅当![]() 时,等号成立)
时,等号成立)
∴![]() 在
在![]() 上单调递增,
上单调递增,
又∵![]() ,∴当
,∴当![]() 时,
时, ![]() ,从而当
,从而当![]() 时,
时, ![]() ,
,
∴![]() 在
在![]() 上单调递减,又∵
上单调递减,又∵![]() ,
,
从而当![]() 时,
时, ![]() ,即
,即![]()
于是当![]() 时,
时, ![]() .
.
(2)当![]() 时,令
时,令![]() ,得
,得![]() ,∴
,∴![]() ,
,
故当![]() 时,
时, ![]() ,
,
∴![]() 在
在![]() 上单调递减,
上单调递减,
又∵![]() ,∴当
,∴当![]() 时,
时, ![]() ,
,
从而当![]() 时,
时, ![]() ,
,
∴![]() 在
在![]() 上单调递增,又∵
上单调递增,又∵![]() ,
,
从而当![]() 时,
时, ![]() ,即
,即![]()
于是当![]() 时,
时, ![]() ,
,
综合得![]() 的取值范围为
的取值范围为![]() .
.
解法二:(Ⅰ)当![]() 时,
时, ![]() ,
,
![]()
![]() ,
,
设直线与曲线![]() 相切,其切点为
相切,其切点为![]() ,
,
则曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,
,
因为切线过点![]() ,所以
,所以![]() ,
,
即![]()
![]() ,
,
∵![]() ,∴
,∴![]()
设![]() ,则
,则![]() ,令
,令![]() 得
得![]()
当![]() 变化时,
变化时, ![]() ,
, ![]() 变化情况如下表:
变化情况如下表:
|
|
|
|
|
|
| + | 0 | - | 0 | + |
| ↗ | 极大值
| ↘ | 极小值 | ↗ |
∴![]() 恰有三个根,
恰有三个根,
故过点![]() 有三条直线与曲线
有三条直线与曲线![]() 相切.
相切.
(Ⅱ)同解法一.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,其中
,其中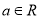 .
.(Ⅰ)给出
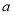 的一个取值,使得曲线
的一个取值,使得曲线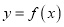 存在斜率为
存在斜率为 的切线,并说明理由;
的切线,并说明理由;(Ⅱ)若
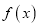 存在极小值和极大值,证明:
存在极小值和极大值,证明: 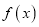 的极小值大于极大值.
的极小值大于极大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
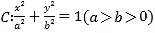 的离心率是
的离心率是 ,且过点
,且过点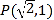 .直线
.直线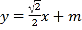 与椭圆
与椭圆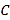 相交于
相交于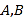 两点.
两点.(Ⅰ)求椭圆
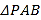 的方程;
的方程;(Ⅱ)求
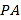 的面积的最大值;
的面积的最大值;(Ⅲ)设直线
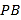 ,
, 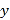 分别与
分别与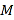 轴交于点
轴交于点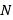 ,
, 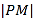 .判断
.判断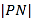 ,
, 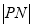 大小关系,并加以证明.
大小关系,并加以证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】某大学为调研学生在
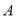 ,
, 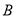 两家餐厅用餐的满意度,从在
两家餐厅用餐的满意度,从在 ,
,  两家餐厅都用过餐的学生中随机抽取了100人,每人分别对这两家餐厅进行评分,满分均为60分.
两家餐厅都用过餐的学生中随机抽取了100人,每人分别对这两家餐厅进行评分,满分均为60分.整理评分数据,将分数以10为组距分成6组:
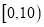 ,
, 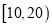 ,
, 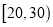 ,
, 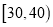 ,
, 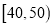 ,
, 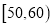 ,得到
,得到 餐厅分数的频率分布直方图,和
餐厅分数的频率分布直方图,和 餐厅分数的频数分布表:
餐厅分数的频数分布表: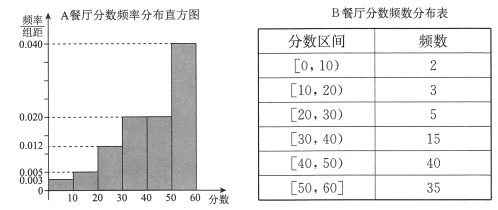
(Ⅰ)在抽样的100人中,求对
 餐厅评分低于30的人数;
餐厅评分低于30的人数;(Ⅱ)从对
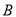 餐厅评分在
餐厅评分在 范围内的人中随机选出2人,求2人中恰有1人评分在
范围内的人中随机选出2人,求2人中恰有1人评分在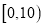 范围内的概率;
范围内的概率;(Ⅲ)如果从
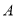 ,
, 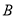 两家餐厅中选择一家用餐,你会选择哪一家?说明理由.
两家餐厅中选择一家用餐,你会选择哪一家?说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
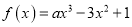 (
(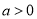 ),定义
),定义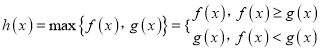 .
.(1)求函数
 的极值
的极值(2)若
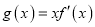 ,且存在
,且存在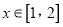 使
使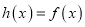 ,求实数
,求实数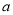 的取值范围;
的取值范围;(3)若
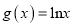 ,试讨论函数
,试讨论函数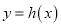 (
(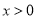 )的零点个数.
)的零点个数. -
科目: 来源: 题型:
查看答案和解析>>【题目】某创业投资公司拟投资开发某种新能源产品,估计能获得10万元到1 000万元的投资收益.现准备制定一个对科研课题组的奖励方案:奖金y(单位:万元)随投资收益x(单位:万元)的增加而增加,且奖金不超过9万元,同时奖金不超过投资收益的20%.
(1)请分析函数y= +1是否符合公司要求的奖励函数模型,并说明原因;
+1是否符合公司要求的奖励函数模型,并说明原因;
(2)若该公司采用函数模型y= 作为奖励函数模型,试确定最小的正整数a的值.
作为奖励函数模型,试确定最小的正整数a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系
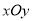 中,以
中,以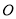 为极点,
为极点, 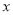 轴的正半轴为极轴建立极坐标系.若直线
轴的正半轴为极轴建立极坐标系.若直线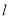 的极坐标方程为
的极坐标方程为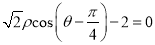 ,曲线
,曲线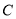 的极坐标方程为
的极坐标方程为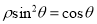 ,将曲线
,将曲线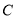 上所有点的横坐标缩短为原来的一半,纵坐标不变,然后再向右平移一个单位得到曲线
上所有点的横坐标缩短为原来的一半,纵坐标不变,然后再向右平移一个单位得到曲线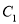 .
.(Ⅰ)求曲线
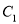 的直角坐标方程;
的直角坐标方程;(Ⅱ)已知直线
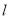 与曲线
与曲线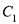 交于
交于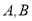 两点,点
两点,点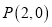 ,求
,求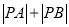 的值.
的值.
相关试题