【题目】已知a为正实数,n为自然数,抛物线 ![]() 与x轴正半轴相交于点A,设f(n)为该抛物线在点A处的切线在y轴上的截距.
与x轴正半轴相交于点A,设f(n)为该抛物线在点A处的切线在y轴上的截距.
(1)用a和n表示f(n);
(2)求对所有n都有 ![]() 成立的a的最小值;
成立的a的最小值;
(3)当0<a<1时,比较 ![]() 与
与 ![]() 的大小,并说明理由.
的大小,并说明理由.
参考答案:
【答案】
(1)解:∵抛物线 ![]() 与x轴正半轴相交于点A,∴A(
与x轴正半轴相交于点A,∴A( ![]() )
)
对 ![]() 求导得y′=﹣2x
求导得y′=﹣2x
∴抛物线在点A处的切线方程为 ![]() ,∴
,∴ ![]()
∵f(n)为该抛物线在点A处的切线在y轴上的截距,∴f(n)=an;
(2)解:由(1)知f(n)=an,则 ![]() 成立的充要条件是an≥2n3+1
成立的充要条件是an≥2n3+1
即知,an≥2n3+1对所有n成立,特别的,取n=2得到a≥ ![]()
当a= ![]() ,n≥3时,an>4n=(1+3)n≥1+
,n≥3时,an>4n=(1+3)n≥1+ ![]() =1+2n3+
=1+2n3+ ![]() >2n3+1
>2n3+1
当n=0,1,2时, ![]()
∴a= ![]() 时,对所有n都有
时,对所有n都有 ![]() 成立
成立
∴a的最小值为 ![]() ;
;
(3)解:由(1)知f(k)=ak,下面证明: ![]()
首先证明:当0<x<1时, ![]()
设函数g(x)= ![]() x(x2﹣x)+1,0<x<1,则g′(x)=
x(x2﹣x)+1,0<x<1,则g′(x)= ![]() x(x﹣
x(x﹣ ![]() )
)
当0<x< ![]() 时,g′(x)<0;当
时,g′(x)<0;当 ![]() 时,g′(x)>0
时,g′(x)>0
故函数g(x)在区间(0,1)上的最小值g(x)min=g( ![]() )=0
)=0
∴当0<x<1时,g(x)≥0,∴ ![]()
由0<a<1知0<ak<1,因此 ![]() ,
,
从而 ![]() =
= ![]() ≥
≥ ![]() =
= ![]() >
> ![]() =
= ![]()
【解析】(1)根据抛物线 ![]() 与x轴正半轴相交于点A,可得A(
与x轴正半轴相交于点A,可得A( ![]() ),进一步可求抛物线在点A处的切线方程,从而可得f(n);(2)由(1)知f(n)=an , 则
),进一步可求抛物线在点A处的切线方程,从而可得f(n);(2)由(1)知f(n)=an , 则 ![]() 成立的充要条件是an≥2n3+1,即知,an≥2n3+1对所有n成立,当a=
成立的充要条件是an≥2n3+1,即知,an≥2n3+1对所有n成立,当a= ![]() ,n≥3时,an>4n=(1+3)n>2n3+1,当n=0,1,2时,
,n≥3时,an>4n=(1+3)n>2n3+1,当n=0,1,2时, ![]() ,由此可得a的最小值;(3)由(1)知f(k)=ak , 证明当0<x<1时,
,由此可得a的最小值;(3)由(1)知f(k)=ak , 证明当0<x<1时, ![]() ,即可证明:
,即可证明: ![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,直线
中,直线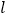 的参数方程为
的参数方程为 (
( 为参数),以原点
为参数),以原点 为极点,
为极点, 轴的非负半轴为极轴且取相同的单位长度建立极坐标系,曲线
轴的非负半轴为极轴且取相同的单位长度建立极坐标系,曲线 的极坐标方程为
的极坐标方程为 .
.(1)求直线
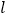 的普通方程及曲线
的普通方程及曲线 的直角坐标方程;
的直角坐标方程;(2)若直线
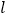 与曲线
与曲线 交于
交于 ,
, 两点,求
两点,求 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某市地产数据研究所的数据显示,2016年该市新建住宅销售均价走势如图所示,3月至7月房价上涨过快,政府从8月采取宏观调控措施,10月份开始房价得到很好的抑制.

(1)地产数据研究所发现,3月至7月的各月均价
 (万元/平方米)与月份
(万元/平方米)与月份 之间具有较强的线性相关关系,试求
之间具有较强的线性相关关系,试求 关于
关于 的回归直线方程;
的回归直线方程;(2)若政府不调控,按照3月份至7月份房价的变化趋势预测12月份该市新建住宅的销售均价.
参考数据:
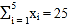 ,
, ,
, ;
;参考公式:
 ,
, .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系
 中,曲线
中,曲线 的参数方程为
的参数方程为 (
( 为参数),以坐标原点
为参数),以坐标原点 为极点,
为极点,  轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线 的极坐标方程为
的极坐标方程为 .
.(1)求曲线
 的普通方程与曲线
的普通方程与曲线 的直角坐标方程;
的直角坐标方程;(2)曲线
 与
与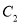 相交于
相交于 两点,求过
两点,求过 两点且面积最小的圆的标准方程.
两点且面积最小的圆的标准方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】设10≤x1<x2<x3<x4≤104 , x5=105 , 随机变量ξ1取值x1、x2、x3、x4、x5的概率均为0.2,随机变量ξ2取值
 、
、  、
、  、
、  、
、  的概率也均为0.2,若记Dξ1、Dξ2分别为ξ1、ξ2的方差,则( )
的概率也均为0.2,若记Dξ1、Dξ2分别为ξ1、ξ2的方差,则( )
A.Dξ1>Dξ2
B.Dξ1=Dξ2
C.Dξ1<Dξ2
D.Dξ1与Dξ2的大小关系与x1、x2、x3、x4的取值有关 -
科目: 来源: 题型:
查看答案和解析>>【题目】设an=
 sin
sin  ,Sn=a1+a2+…+an , 在S1 , S2 , …S100中,正数的个数是( )
,Sn=a1+a2+…+an , 在S1 , S2 , …S100中,正数的个数是( )
A.25
B.50
C.75
D.100 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD与BC是四面体ABCD中互相垂直的棱,BC=2,若AD=2c,且AB+BD=AC+CD=2a,其中a、c为常数,则四面体ABCD的体积的最大值是 .

相关试题

