搜索
【题目】△ABC的内角A，B，C的对边分别是a，b，c，且2acosA＝bcosC＋ccosB.
(Ⅰ)求A的大小；
(Ⅱ)若a＝2，求b＋c的取值范围．
参考答案：
【答案】(Ⅰ) A＝
(Ⅱ) 
【解析】试题分析：（Ⅰ）通过正弦定理化简式子并分离出
利用两角和的正弦函数化简求值，再求出
的大小；
（Ⅱ）通过余弦定理以及基本不等式求出
的范围，再利用三角形三边的关系求出
的范围．
试题解析：(Ⅰ)∵2acosA＝bcosC＋ccosB ，
∴2sinAcosA＝sinBcosC＋sinCcosB ，
即cosA＝
＝
＝
，A∈(0，π)，∴A＝
；
(Ⅱ)由余弦定理知4＝b2＋c2－bc，
∴4≥2
2－
2＝
2，∴b＋c≤4，
又∵b＋c>a，∴b＋c>2，
综上，b＋c的取值范围为
.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，菱形
与等边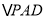
所在的平面相互垂直， 
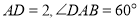，点E，F分别为PC和AB的中点．（Ⅰ）求证：EF∥平面PAD
（Ⅱ）证明：
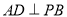；（Ⅲ）求三棱锥
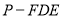的体积．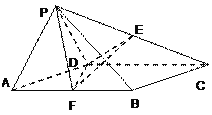
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知
（
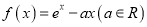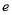为自然对数的底数）．（Ⅰ）讨论
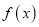的单调性；（Ⅱ）若
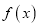有两个零点
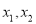，求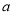
的取值范围；（2）在（1）的条件下，求证：
． -
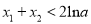科目： 来源： 题型：
查看答案和解析>>【题目】选修4—4：坐标系与参数方程
在直角坐标系
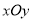中，直线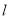
的参数方程为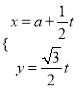
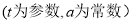．以坐标原点为极点，以
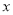轴的正半轴为极轴，建立极坐标系，曲线
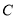的极坐标方程为
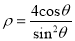．（Ⅰ）写出
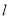的普通方程和
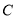的直角坐标方程；（Ⅱ）设直线
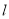与曲线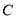
交于A,B两点，当
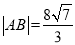时，求
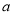的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知四棱锥P－ABCD中，PD⊥平面ABCD，ABCD是正方形，E是PA的中点．
(Ⅰ)求证：PC∥平面EBD；
(Ⅱ)求证：平面PBC⊥平面PCD.
-
科目： 来源： 题型：
查看答案和解析>>【题目】家政服务公司根据用户满意程度将本公司家政服务员分为两类，其中A类服务员12名，B类服务员x名．
(Ⅰ)若采用分层抽样的方法随机抽取20名家政服务员参加技术培训，抽取到B类服务员的人数是16, 求x的值；
(Ⅱ)某客户来公司聘请2名家政服务员，但是由于公司人员安排已经接近饱和，只有3名A类家政服务员和2名B类家政服务员可供选择，求该客户最终聘请的家政服务员中既有A类又有B类的概率．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知椭圆C：
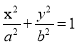(a>b>0)，长轴长为4，离心率为
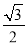.(Ⅰ)椭圆的求椭圆的标准方程；
(Ⅱ)设过定点M(0,2)的直线l与椭圆C交于不同的两点A，B，且∠AOB为锐角(O为坐标原点)，求直线l的斜率k的取值范围．
相关试题
