【题目】如图,在棱长为![]() 的正方体
的正方体![]() 中,点
中,点![]() 、
、![]() 是棱
是棱![]() 、
、![]() 的中点,
的中点, ![]() 是底面
是底面![]() 上(含边界)一动点,满足
上(含边界)一动点,满足![]() ,则线段
,则线段![]() 长度的取值范围是( )
长度的取值范围是( )

A.  B.
B.  C.
C. ![]() D.
D. ![]()
参考答案:
【答案】D
【解析】因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以
,所以 ![]()
![]() ,又因为
,又因为![]() 所以可得
所以可得![]() 平面
平面![]() ,当点
,当点![]() 在线段
在线段![]() 上时,总有
上时,总有![]() ,所以
,所以![]() 的最大值为
的最大值为![]() ,
, ![]() 的最小值为
的最小值为![]() ,可得线段
,可得线段![]() 长度的取值范围是
长度的取值范围是![]() ,故选D.
,故选D.
【方法点晴】本题主要考查正方体的性质、线面垂直的判定定理的应用,属于难题.解答空间几何体中垂直关系时,一般要根据已知条件把空间中的线线、线面、面面之间垂直关系进行转化,转化时要正确运用有关的定理,找出足够的条件进行推理;证明直线和平面垂直的常用方法有:(1)利用判定定理;(2)利用判定定理的推论![]() ;(3)利用面面平行的性质
;(3)利用面面平行的性质![]() ;(4)利用面面垂直的性质,当两个平面垂直时,在一个平面内垂直于交线的直线垂直于另一个平面.
;(4)利用面面垂直的性质,当两个平面垂直时,在一个平面内垂直于交线的直线垂直于另一个平面.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在底面是正方形的四棱锥
 中,
中,  ,
,  ,点
,点 在
在 上,且
上,且 .
.
(Ⅰ)求证:
 平面
平面 ;
;(Ⅱ)求二面角
 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
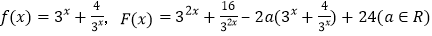 .
.(1)若函数
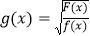 的值域为[0,+∞),求实数a的取值范围;
的值域为[0,+∞),求实数a的取值范围;(2)若关于x的不等式F(x)>af(x)+12恒成立,求实数a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=ex﹣ax﹣1(a为常数),曲线y=f(x)在与y轴的交点A处的切线斜率为﹣1.
(1)求a的值及函数y=f(x)的单调区间;
(2)若x1<ln2,x2>ln2,且f(x1)=f(x2),证明:x1+x2<2ln2. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 为奇函数.
为奇函数.(1)求
 的值;
的值;(2)求函数
 在
在 的最小值;
的最小值;(3)若函数
 在区间
在区间 上单调递减,求实数
上单调递减,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设
 .
.(1)在图的直角坐标系中画出f(x)的图象;
(2)若f(t)=2,求t值;
(3)求函数f(x)的最小值.

-
科目: 来源: 题型:
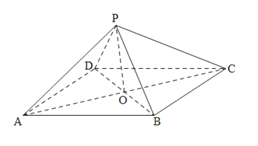
查看答案和解析>>【题目】如图,在四棱锥
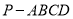 中,四边形
中,四边形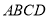 是平行四边形,
是平行四边形, 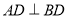 且
且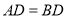 ,
, 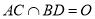 ,
, 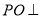 平面
平面 .
.
(1)
 为棱
为棱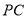 的中点,求证:
的中点,求证: 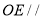 平面
平面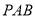 ;
;(2)求证: 平面
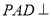 平面
平面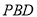 ;
;(3)若
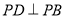 ,
, 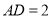 ,求四棱锥
,求四棱锥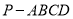 的体积.
的体积.
相关试题

