【题目】已知![]() .
.
(1)当![]() 为何值时,
为何值时, ![]() 最小? 此时
最小? 此时![]() 与
与![]() 的位置关系如何?
的位置关系如何?
(2)当![]() 为何值时,
为何值时, ![]() 与
与![]() 的夹角最小? 此时
的夹角最小? 此时![]() 与
与![]() 的位置关系如何?
的位置关系如何?
参考答案:
【答案】(1) 当![]() 时,
时, ![]() 最小,
最小, ![]() ;(2)
;(2)![]() 时,
时, ![]() 与
与![]() 的夹角最小,
的夹角最小, ![]() 与
与![]() 平行.
平行.
【解析】试题分析:(1)由向量的坐标运算,可将![]() 表示成关于
表示成关于![]() 的二次函数,利用二次函数的最值求得
的二次函数,利用二次函数的最值求得![]() 何时求最小值.由
何时求最小值.由![]() 求得
求得![]() ,进一步可得两者位置关系;(2)由
,进一步可得两者位置关系;(2)由![]() 的坐标运算,转化为关于
的坐标运算,转化为关于![]() 的表达式,由夹角最小时,余弦值最大为
的表达式,由夹角最小时,余弦值最大为![]() ,可得关于
,可得关于![]() 的方程,解得
的方程,解得![]() ,再求得此时
,再求得此时![]() 与
与![]() 的坐标,可判断两者的位置关系.
的坐标,可判断两者的位置关系.
试题解析:
(1)![]() ,
,
![]()
![]()
当![]() 时,
时, ![]() 最小,此时
最小,此时![]() ,
,![]() , ∴
, ∴![]()
∴当![]() 时,
时, ![]() 最小,此时
最小,此时![]() .
.
(2)设![]() 与
与![]() 的夹角为
的夹角为![]() ,则
,则![]() ,
,
要![]() 与
与![]() 的夹角最小,则
的夹角最小,则![]() 最大, ∵
最大, ∵![]() ,故
,故![]() 的最大值为
的最大值为![]() ,此时
,此时![]() ,
,
![]() ,解之得
,解之得![]() ,
,![]() .
.
∴![]() 时,
时, ![]() 与
与![]() 的夹角最小, 此时
的夹角最小, 此时![]() 与
与![]() 平行.
平行.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 的图象如图所示.
的图象如图所示.
(Ⅰ)求
 的值;
的值;(Ⅱ)若函数
 在
在 处的切线方程为
处的切线方程为 ,求函数
,求函数 的解析式;
的解析式;(Ⅲ)在(Ⅱ)的条件下,函数
 与
与 的图象有三个不同的交点,求
的图象有三个不同的交点,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校从参加高三模拟考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[90,100),[100,110),…,[140,150)后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
求分数在[120,130)内的频率,并补全这个频
率分布直方图;
统计方法中,同一组数据常用该组区间的中点
值作为代表,据此估计本次考试的平均分;
(3)用分层抽样的方法在分数段为[110,130)的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任取2个,求至多有1人在分数段[120,130)内的概率.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一名学生每天骑车上学,从他家里到学校的途中有6个交通岗,假设在每个交通岗遇到红灯的事件是相互独立的,并且概率都是
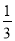 .
.(1)假设
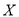 为这名学生在途中遇到红灯的次数,求
为这名学生在途中遇到红灯的次数,求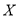 的分布列;
的分布列;(2)设
 为这名学生在首次停车前经过的路口数,求
为这名学生在首次停车前经过的路口数,求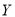 的分布列;
的分布列; -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
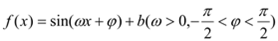 相邻两对称轴间的距离为
相邻两对称轴间的距离为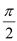 ,若将
,若将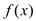 的图像先向左平移
的图像先向左平移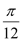 个单位,再向下平移1个单位,所得的函数
个单位,再向下平移1个单位,所得的函数 为奇函数.
为奇函数.(1)求
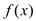 的解析式,并求
的解析式,并求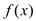 的对称中心;
的对称中心;(2)若关于
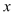 的方程
的方程 在区间
在区间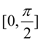 上有两个不相等的实根,求实数
上有两个不相等的实根,求实数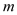 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直四棱柱
 中,
中,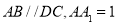 ,
,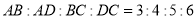 ,侧棱
,侧棱 底面
底面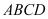 .
.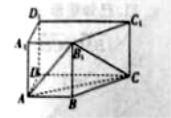
(I)证明:平面
 平面
平面 ;
;(II)若直线
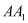 与平面
与平面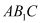 所成的角的余弦值为
所成的角的余弦值为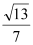 ,求
,求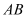 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙、丙三台机床各自独立地加工同一种零件,已知甲机床加工的零件是一等品而乙机床加工的零件不是一等品的概率是
 ,乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率是
,乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率是 ,甲、乙两台机床加工的零件都是一等品的概率是
,甲、乙两台机床加工的零件都是一等品的概率是 .
.(1)分别求甲、乙、丙三台机床各自加工的零件是一等品的概率;
(2)从甲、乙、丙三台机床加工的零件中各取一个检验,求至少有一个一等品的概率;
相关试题

