【题目】已知函数f(x)是定义在[﹣1,1]上的奇函数,且f(1)=1,若x,y∈[﹣1,1],x+y≠0有(x+y)[f(x)+f(y)]>0.
(1)判断f(x)的单调性,并加以证明;
(2)解不等式 ![]() ;
;
(3)若f(x)≤m2﹣2am+1对所有x∈[﹣1,1],a∈[﹣1,1]恒成立.求实数m的取值范围.
参考答案:
【答案】
(1)解:函数f(x)在[﹣1,1]上单调增,证明如下
由题意,设x1,x2∈[﹣1,1],且x1<x2
则x1﹣x2<0
∵x,y∈[﹣1,1],x+y≠0有(x+y)[f(x)+f(y)]>0.
令x=x1,y=﹣x2,
∴f(x1)+f(﹣x2)<0
∵函数f(x)是定义在[﹣1,1]上的奇函数
∴f(x1)﹣f(x2)<0
∴函数f(x)在[﹣1,1]上单调增
(2)解:由(1)知, ![]() ,解得:
,解得: ![]()
(3)解:由于函数f(x)在[﹣1,1]上单调增,
∴函数f(x)在[﹣1,1]上的最大值为f(1)=1
∴f(x)≤m2﹣2am+1对所有x∈[﹣1,1],a∈[﹣1,1]恒成立可转化为:0≤m2﹣2am对所有a∈[﹣1,1]恒成立
∴ ![]() ,
,
解得m≥2或m≤﹣2或m=0
【解析】(1)设x1 , x2∈[﹣1,1],且x1<x2 , 则x1﹣x2<0,利用x,y∈[﹣1,1],x+y≠0有(x+y)[f(x)+f(y)]>0,可得f(x1)+f(﹣x2)<0,根据函数f(x)是定义在[﹣1,1]上的奇函数,即可得函数f(x)在[﹣1,1]上单调增;(2)由(1)知, ![]() ,解之即可;(3)先确定函数f(x)在[﹣1,1]上的最大值为f(1)=1,将f(x)≤m2﹣2am+1对所有x∈[﹣1,1],a∈[﹣1,1]恒成立转化为:0≤m2﹣2am对所有a∈[﹣1,1]恒成立,从而可求实数m的取值范围.
,解之即可;(3)先确定函数f(x)在[﹣1,1]上的最大值为f(1)=1,将f(x)≤m2﹣2am+1对所有x∈[﹣1,1],a∈[﹣1,1]恒成立转化为:0≤m2﹣2am对所有a∈[﹣1,1]恒成立,从而可求实数m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆C:(x﹣3)2+(y﹣4)2=4,直线l过定点A(1,0).
(1)若l与圆C相切,求l的方程;
(2)若l与圆C相交于P、Q两点,若|PQ|=2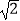 ,求此时直线l的方程.
,求此时直线l的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知点A(1,0),D(﹣1,0),点B,C在单位圆O上,且∠BOC=
 .
. 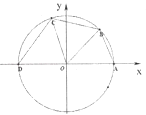
(Ⅰ)若点B(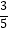 ,
, 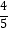 ),求cos∠AOC的值;
),求cos∠AOC的值;
(Ⅱ)设∠AOB=x(0<x<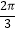 ),四边形ABCD的周长为y,将y表示成x的函数,并求出y的最大值.
),四边形ABCD的周长为y,将y表示成x的函数,并求出y的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的几何体中,四边形ABCD是平行四边形,∠ABD=90°,EB⊥平面ABCD,EF∥AB,AB=2,EB=
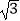 ,EF=1,BC=
,EF=1,BC= 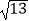 ,且M是BD的中点..
,且M是BD的中点.. 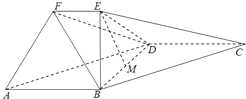
(1)求证:EM∥平面ADF;
(2)求直线DF和平面ABCD所成角的正切值;
(3)求二面角D﹣AF﹣B的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线C:y2=2px过点P(1,1).过点(0,
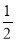 )作直线l与抛物线C交于不同的两点M,N,过点M作x轴的垂线分别与直线OP、ON交于点A,B,其中O为原点.
)作直线l与抛物线C交于不同的两点M,N,过点M作x轴的垂线分别与直线OP、ON交于点A,B,其中O为原点.(Ⅰ)求抛物线C的方程,并求其焦点坐标和准线方程;
(Ⅱ)求证:A为线段BM的中点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥P﹣ABCD中,所有棱长均为2,O是底面正方形ABCD中心,E为PC中点,则直线OE与直线PD所成角为( )

A.30°
B.60°
C.45°
D.90° -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
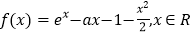
(Ⅰ)若
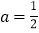 ,求函数
,求函数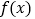 的单调区间;
的单调区间;(Ⅱ)若对任意
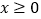 都有
都有 恒成立,求实数
恒成立,求实数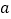 的取值范围;
的取值范围;(Ⅲ)设函数
 ,求证:
,求证: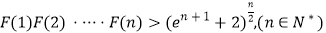
.
相关试题

