【题目】如图,在四棱锥![]() 中,在底面
中,在底面![]() 中,
中, ![]() 是
是![]() 的中点,
的中点, ![]() 是棱
是棱![]() 的中点,
的中点, ![]() =
= ![]() =
= ![]() =
= ![]() =
= ![]() =
= ![]() =
=![]() .
.
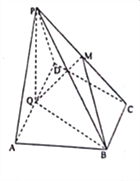
(1)求证: ![]() 平面
平面![]()
(2)求证:平面![]() 底面
底面![]() ;
;
(3)试求三棱锥![]() 的体积.
的体积.
参考答案:
【答案】(1)见解析;(2)见解析;(3)![]() .
.
【解析】试题分析:(1)连接![]() ,交BQ于N,连接MN,证明
,交BQ于N,连接MN,证明![]() 即可,
即可,
(2)根据面面垂直的判定定理,先证明![]() ,即可,
,即可,
(3)先证明![]() 平面
平面![]() ,再根据
,再根据![]() =
=![]() =
=![]() ,即可解答.
,即可解答.
试题解析:
(1) 如图,连接![]() ,交BQ于N,连接MN,
,交BQ于N,连接MN,
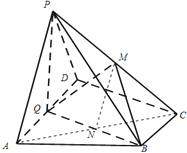
∵![]() =
= ![]() ,是
,是![]() 的中点,
的中点,
∴![]() ,且
,且![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∴N是BQ中点,
∵![]() 是棱
是棱![]() 的中点,
的中点,
∴![]() ,
,
∵PA![]() 平面
平面![]() 平面
平面![]() .
.
∴![]() 平面
平面![]()
(2)证明: ![]()
![]() 是
是![]() 的中点
的中点
![]() 四边形
四边形![]() 为平行四边形,
为平行四边形,
![]() ,
,
![]() .
.
又![]()
故![]()
又![]()
![]() ,
,
由勾股定理可知![]() ,
,
又![]() ,
,
![]() ,又
,又![]() 平面
平面![]() ,
,
![]() 平面
平面![]() 平面
平面![]() .
.
(3) ![]() 是
是![]() 的中点,
的中点,
![]() ,
,
![]() 平面
平面![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
又![]() 是棱
是棱![]() 上的中点,故
上的中点,故
![]() =
=![]() =
=![]() =
=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“一带一路”是“丝绸之路经济带”和“21世纪海上丝绸之路”的简称.某市为了了解人们对“一带一路”的认知程度,对不同年龄和不同职业的人举办了一次“一带一路”知识竞赛,满分100分(90分及以上为认知程度高).现从参赛者中抽取了
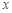 人,按年龄分成5组,第一组:
人,按年龄分成5组,第一组: 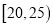 ,第二组:
,第二组: 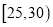 ,第三组:
,第三组: 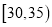 ,第四组:
,第四组: 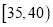 ,第五组:
,第五组: 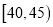 ,得到如图所示的频率分布直方图,已知第一组有6人.
,得到如图所示的频率分布直方图,已知第一组有6人.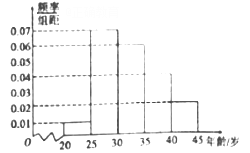
(1)求
 ;
;(2)求抽取的
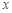 人的年龄的中位数(结果保留整数);
人的年龄的中位数(结果保留整数);(3)从该市大学生、军人、医务人员、工人、个体户 五种人中用分层抽样的方法依次抽取6人,42人,36人,24人,12人,分别记为1~5组,从这5个按年龄分的组和5个按职业分的组中每组各选派1人参加知识竞赛,分别代表相应组的成绩,年龄组中1~5组的成绩分别为93,96,97,94,90,职业组中1~5组的成绩分别为93,98,94,95,90.
(Ⅰ)分别求5个年龄组和5个职业组成绩的平均数和方差;
(Ⅱ)以上述数据为依据,评价5个年龄组和5个职业组对“一带一路”的认知程度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于区间
 ,若函数
,若函数 同时满足:①
同时满足:① 在
在 上是单调函数;②函数
上是单调函数;②函数 ,
, 的值域是
的值域是 ,则称区间
,则称区间 为函数
为函数 的“保值”区间.
的“保值”区间.(1)求函数
 的所有“保值”区间.
的所有“保值”区间.(2)函数
 是否存在“保值”区间?若存在,求出
是否存在“保值”区间?若存在,求出 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
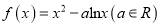 .
.(1)当
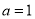 时,求函数
时,求函数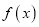 在点
在点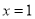 处的切线方程;
处的切线方程;(2)求函数
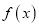 的极值;
的极值;(3)若函数
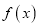 在区间
在区间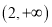 上是增函数,试确定
上是增函数,试确定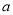 的取值范围.
的取值范围.【答案】(1)
 ;(2)当
;(2)当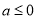 时,
时, 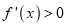 恒成立,
恒成立, 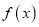 不存在极值.当
不存在极值.当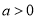 时,
时, 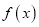 有极小值
有极小值 无极大值.(3)
无极大值.(3)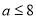 .
.【解析】试题分析:
(1)当
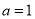 时,求得
时,求得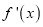 ,得到
,得到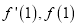 的值,即可求解切线方程.
的值,即可求解切线方程.(2)由定义域为
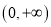 ,求得
,求得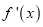 ,分
,分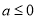 和
和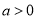 时分类讨论得出函数的单调区间,即可求解函数的极值.
时分类讨论得出函数的单调区间,即可求解函数的极值.(3)根据题意
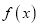 在
在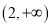 上递增,得
上递增,得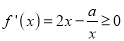 对
对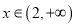 恒成立,进而求解实数
恒成立,进而求解实数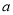 的取值范围.
的取值范围.试题解析:
(1)当
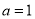 时,
时, 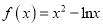 ,
,  ,
,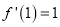 ,又
,又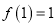 ,∴切线方程为
,∴切线方程为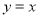 .
.(2)定义域为
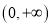 ,
, 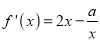 ,当
,当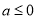 时,
时, 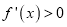 恒成立,
恒成立,  不存在极值.
不存在极值.当
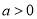 时,令
时,令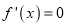 ,得
,得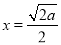 ,当
,当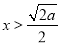 时,
时, 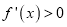 ;当
;当 时,
时, 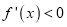 ,
,所以当
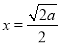 时,
时, 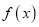 有极小值
有极小值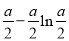 无极大值.
无极大值.(3)∵
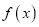 在
在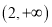 上递增,∴
上递增,∴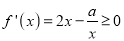 对
对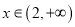 恒成立,即
恒成立,即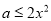 恒成立,∴
恒成立,∴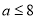 .
.点睛:导数是研究函数的单调性、极值(最值)最有效的工具,而函数是高中数学中重要的知识点,所以在历届高考中,对导数的应用的考查都非常突出 ,本专题在高考中的命题方向及命题角度 从高考来看,对导数的应用的考查主要从以下几个角度进行: (1)考查导数的几何意义,往往与解析几何、微积分相联系. (2)利用导数求函数的单调区间,判断单调性;已知单调性,求参数. (3)考查数形结合思想的应用.
【题型】解答题
【结束】
22【题目】已知圆
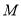 :
:  和点
和点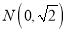 ,
, 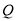 是圆
是圆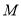 上任意一点,线段
上任意一点,线段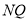 的垂直平分线和
的垂直平分线和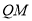 相交于点
相交于点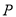 ,
, 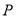 的轨迹为曲线
的轨迹为曲线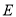 .
.(1)求曲线
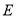 的方程;
的方程;(2)点
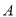 是曲线
是曲线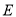 与
与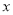 轴正半轴的交点,直线
轴正半轴的交点,直线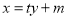 交
交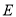 于
于 、
、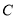 两点,直线
两点,直线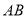 ,
, 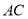 的斜率分别是
的斜率分别是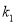 ,
, 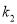 ,若
,若 ,求:①
,求:①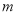 的值;②
的值;②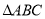 面积的最大值.
面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分12分)
在
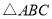 中,内角
中,内角 对边的边长分别是
对边的边长分别是 ,已知
,已知 ,
, .
.(Ⅰ)若
 的面积等于
的面积等于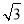 ,求
,求 ;
;(Ⅱ)若
 ,求
,求 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,
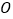 为坐标原点,已知向量
为坐标原点,已知向量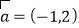 ,又点
,又点 ,
,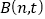 ,
, ,
,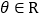 .
.(1)若
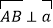 ,且
,且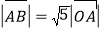 ,求向量
,求向量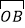 ;
;(2)若向量
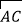 与向量
与向量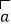 共线,常数
共线,常数 ,求
,求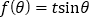 的值域.
的值域. -
科目: 来源: 题型:
查看答案和解析>>【题目】共享汽车的出现为我们的出行带来了极大的便利,当然也为投资商带来了丰厚的利润。现某公司瞄准这一市场,准备投放共享汽车。该公司取得了在
 个省份投放共享汽车的经营权,计划前期一次性投入
个省份投放共享汽车的经营权,计划前期一次性投入 元. 设在每个省投放共享汽车的市的数量相同(假设每个省的市的数量足够多),每个市都投放
元. 设在每个省投放共享汽车的市的数量相同(假设每个省的市的数量足够多),每个市都投放 辆共享汽车.由于各个市的多种因素的差异,在第
辆共享汽车.由于各个市的多种因素的差异,在第 个市的每辆共享汽车的管理成本为(
个市的每辆共享汽车的管理成本为( )元(其中
)元(其中 为常数).经测算,若每个省在
为常数).经测算,若每个省在 个市投放共享汽车,则该公司每辆共享汽车的平均综合管理费用为
个市投放共享汽车,则该公司每辆共享汽车的平均综合管理费用为 元.(本题中不考虑共享汽车本身的费用)
元.(本题中不考虑共享汽车本身的费用)注:综合管理费用=前期一次性投入的费用+所有共享汽车的管理费用,平均综合管理费用=综合管理费用÷共享汽车总数.
(1)求
 的值;
的值;(2)问要使该公司每辆共享汽车的平均综合管理费用最低,则每个省有几个市投放共享汽车?此时每辆共享汽车的平均综合管理费用为多少元?
相关试题

