【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)求函数![]() 的极值;
的极值;
(3)若函数![]() 在区间
在区间![]() 上是增函数,试确定
上是增函数,试确定![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)当
;(2)当![]() 时,
时, ![]() 恒成立,
恒成立, ![]() 不存在极值.当
不存在极值.当![]() 时,
时,
![]() 有极小值
有极小值![]() 无极大值.(3)
无极大值.(3)![]() .
.
【解析】试题分析:
(1)当![]() 时,求得
时,求得![]() ,得到
,得到![]() 的值,即可求解切线方程.
的值,即可求解切线方程.
(2)由定义域为![]() ,求得
,求得![]() ,分
,分![]() 和
和![]() 时分类讨论得出函数的单调区间,即可求解函数的极值.
时分类讨论得出函数的单调区间,即可求解函数的极值.
(3)根据题意![]() 在
在![]() 上递增,得
上递增,得![]() 对
对![]() 恒成立,进而求解实数
恒成立,进而求解实数![]() 的取值范围.
的取值范围.
试题解析:
(1)当![]() 时,
时, ![]() ,
, ![]() ,
,
![]() ,又
,又![]() ,∴切线方程为
,∴切线方程为![]() .
.
(2)定义域为![]() ,
, ![]() ,当
,当![]() 时,
时, ![]() 恒成立,
恒成立, ![]() 不存在极值.
不存在极值.
当![]() 时,令
时,令![]() ,得
,得![]() ,当
,当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() ,
,
所以当![]() 时,
时, ![]() 有极小值
有极小值![]() 无极大值.
无极大值.
(3)∵![]() 在
在![]() 上递增,∴
上递增,∴![]() 对
对![]() 恒成立,即
恒成立,即![]() 恒成立,∴
恒成立,∴![]() .
.
点睛:导数是研究函数的单调性、极值(最值)最有效的工具,而函数是高中数学中重要的知识点,所以在历届高考中,对导数的应用的考查都非常突出 ,本专题在高考中的命题方向及命题角度 从高考来看,对导数的应用的考查主要从以下几个角度进行: (1)考查导数的几何意义,往往与解析几何、微积分相联系. (2)利用导数求函数的单调区间,判断单调性;已知单调性,求参数. (3)考查数形结合思想的应用.
【题型】解答题
【结束】
22
【题目】已知圆![]() :
: ![]() 和点
和点![]() ,
, ![]() 是圆
是圆![]() 上任意一点,线段
上任意一点,线段![]() 的垂直平分线和
的垂直平分线和![]() 相交于点
相交于点![]() ,
, ![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)点![]() 是曲线
是曲线![]() 与
与![]() 轴正半轴的交点,直线
轴正半轴的交点,直线![]() 交
交![]() 于
于![]() 、
、![]() 两点,直线
两点,直线![]() ,
, ![]() 的斜率分别是
的斜率分别是![]() ,
, ![]() ,若
,若![]() ,求:①
,求:①![]() 的值;②
的值;②![]() 面积的最大值.
面积的最大值.
参考答案:
【答案】(1)![]() ;(2)①
;(2)①![]() ②
②![]() .
.
【解析】试题分析:
(1)由圆的方程得圆心为![]() ,半径为
,半径为![]() ,可得,
,可得, ![]() ,
,
所以曲线![]() 是
是![]() ,
, ![]() 为焦点,长轴长为
为焦点,长轴长为![]() 的椭圆,即可求解椭圆的方程;
的椭圆,即可求解椭圆的方程;
(2)①由直线方程和椭圆的方程联立方程组,由![]() ,解得
,解得![]() ,
, ![]() ,根据
,根据![]() ,化简得即可解得
,化简得即可解得![]() 的值;
的值;
②由题意![]() ,利用均值不等式,即可求解
,利用均值不等式,即可求解![]() 面积的最大值.
面积的最大值.
试题解析:
(1)圆![]() :
: ![]() 的圆心为
的圆心为![]() ,半径为
,半径为![]() ,点
,点![]()
![]() 在圆
在圆![]() 内,
内, ![]() ,
,
所以曲线![]() 是
是![]() ,
, ![]() 为焦点,长轴长为
为焦点,长轴长为![]() 的椭圆,
的椭圆,
由![]() ,
, ![]() ,得
,得![]() ,所以曲线
,所以曲线![]() 的方程为
的方程为![]() .
.
(2)①设![]() ,
, ![]() ,直线
,直线![]() :
: ![]() ,联立方程组
,联立方程组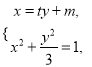 得
得
![]() ,
,
由![]() ,解得
,解得![]() ,
, ![]() ,
, ![]() ,
,
由![]() 知
知![]()
![]() ,
,
且![]() ,代入化简得
,代入化简得![]() ,解得
,解得![]() ,
,
②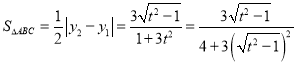
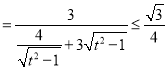 (当且仅当
(当且仅当![]() 时取等号).
时取等号).
综上, ![]() 面积的最大值为
面积的最大值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,底面
中,底面 是平行四边形,
是平行四边形,  ,侧面
,侧面 底面
底面 ,
,  ,
,  ,
,  ,
,  分别为
分别为 ,
,  的中点,点
的中点,点 在线段
在线段 上.
上.
(1)求证:
 平面
平面 ;
;(2)如果三棱锥
 的体积为
的体积为 ,求点
,求点 到面
到面 的距离.
的距离.【答案】(1)证明见解析;(2)
 .
.【解析】试题分析:
(1)在平行四边形
 中,得出
中,得出 ,进而得到
,进而得到 ,证得
,证得 底面
底面 ,得出
,得出 ,进而证得
,进而证得 平面
平面 .
.(2)由
 到面
到面 的距离为
的距离为 ,所以
,所以 面
面 ,
,  为
为 中点,即可求解
中点,即可求解 的值.
的值.试题解析:
证明:(1)在平行四边形
 中,因为
中,因为 ,
,  ,
,所以
 ,由
,由 ,
,  分别为
分别为 ,
,  的中点,得
的中点,得 ,所以
,所以 .
.侧面
 底面
底面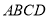 ,且
,且 ,
,  底面
底面 .
.又因为
 底面
底面 ,所以
,所以 .
.又因为
 ,
,  平面
平面 ,
,  平面
平面 ,
,所以
 平面
平面 .
.解:(2)
 到面
到面 的距离为1,所以
的距离为1,所以 面
面 ,
,  为
为 中点,
中点,  .
.【题型】解答题
【结束】
21【题目】已知函数
 .
.(1)当
 时,求函数
时,求函数 在点
在点 处的切线方程;
处的切线方程;(2)求函数
 的极值;
的极值;(3)若函数
 在区间
在区间 上是增函数,试确定
上是增函数,试确定 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】“一带一路”是“丝绸之路经济带”和“21世纪海上丝绸之路”的简称.某市为了了解人们对“一带一路”的认知程度,对不同年龄和不同职业的人举办了一次“一带一路”知识竞赛,满分100分(90分及以上为认知程度高).现从参赛者中抽取了
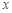 人,按年龄分成5组,第一组:
人,按年龄分成5组,第一组: 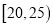 ,第二组:
,第二组: 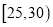 ,第三组:
,第三组: 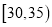 ,第四组:
,第四组: 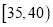 ,第五组:
,第五组: 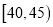 ,得到如图所示的频率分布直方图,已知第一组有6人.
,得到如图所示的频率分布直方图,已知第一组有6人.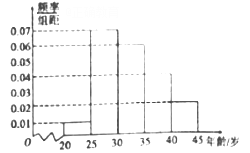
(1)求
 ;
;(2)求抽取的
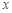 人的年龄的中位数(结果保留整数);
人的年龄的中位数(结果保留整数);(3)从该市大学生、军人、医务人员、工人、个体户 五种人中用分层抽样的方法依次抽取6人,42人,36人,24人,12人,分别记为1~5组,从这5个按年龄分的组和5个按职业分的组中每组各选派1人参加知识竞赛,分别代表相应组的成绩,年龄组中1~5组的成绩分别为93,96,97,94,90,职业组中1~5组的成绩分别为93,98,94,95,90.
(Ⅰ)分别求5个年龄组和5个职业组成绩的平均数和方差;
(Ⅱ)以上述数据为依据,评价5个年龄组和5个职业组对“一带一路”的认知程度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于区间
 ,若函数
,若函数 同时满足:①
同时满足:① 在
在 上是单调函数;②函数
上是单调函数;②函数 ,
, 的值域是
的值域是 ,则称区间
,则称区间 为函数
为函数 的“保值”区间.
的“保值”区间.(1)求函数
 的所有“保值”区间.
的所有“保值”区间.(2)函数
 是否存在“保值”区间?若存在,求出
是否存在“保值”区间?若存在,求出 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由. -
科目: 来源: 题型:
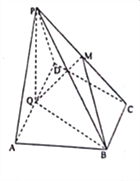
查看答案和解析>>【题目】如图,在四棱锥
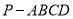 中,在底面
中,在底面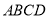 中,
中,  是
是 的中点,
的中点, 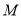 是棱
是棱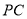 的中点,
的中点, 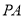 =
= 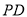 =
=  =
= 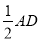 =
= 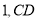 =
=  =
=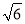 .
.
(1)求证:
 平面
平面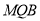
(2)求证:平面
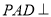 底面
底面 ;
;(3)试求三棱锥
 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分12分)
在
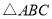 中,内角
中,内角 对边的边长分别是
对边的边长分别是 ,已知
,已知 ,
, .
.(Ⅰ)若
 的面积等于
的面积等于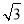 ,求
,求 ;
;(Ⅱ)若
 ,求
,求 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,
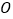 为坐标原点,已知向量
为坐标原点,已知向量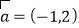 ,又点
,又点 ,
,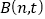 ,
, ,
,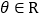 .
.(1)若
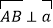 ,且
,且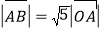 ,求向量
,求向量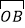 ;
;(2)若向量
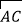 与向量
与向量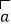 共线,常数
共线,常数 ,求
,求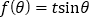 的值域.
的值域.
相关试题

