【题目】已知函数f(x)=2sinωxcosωx+2 ![]() sin2ωx﹣
sin2ωx﹣ ![]() (ω>0)的最小正周期为π. (Ⅰ)求函数f(x)的单调增区间;
(ω>0)的最小正周期为π. (Ⅰ)求函数f(x)的单调增区间;
(Ⅱ)将函数f(x)的图象向左平移 ![]() 个单位,再向上平移1个单位,得到函数y=g(x)的图象.若y=g(x)在[0,b](b>0)上至少含有10个零点,求b的最小值.
个单位,再向上平移1个单位,得到函数y=g(x)的图象.若y=g(x)在[0,b](b>0)上至少含有10个零点,求b的最小值.
参考答案:
【答案】解:(Ⅰ)由题意,可得
f(x)= ![]() =
= ![]() .
.
∵函数的最小正周期为π,∴ ![]() =π,解之得ω=1.
=π,解之得ω=1.
由此可得函数的解析式为 ![]() .
.
令 ![]() ,解之得
,解之得 ![]()
∴函数f(x)的单调增区间是 ![]() .
.
(Ⅱ)将函数f(x)的图象向左平移 ![]() 个单位,再向上平移1个单位,可得函数y=f(x+
个单位,再向上平移1个单位,可得函数y=f(x+ ![]() )+1的图象,
)+1的图象,
∵ ![]()
∴g(x)= ![]() +1=2sin2x+1,可得y=g(x)的解析式为g(x)=2sin2x+1.
+1=2sin2x+1,可得y=g(x)的解析式为g(x)=2sin2x+1.
令g(x)=0,得sin2x=﹣ ![]() ,可得2x=
,可得2x= ![]() 或2x=
或2x= ![]()
解之得 ![]() 或
或 ![]() .
.
∴函数g(x)在每个周期上恰有两个零点,
若y=g(x)在[0,b]上至少含有10个零点,则b不小于第10个零点的横坐标即可,
即b的最小值为 ![]() .
.
【解析】(I)根据二倍角的三角函数公式与辅助角公式化简得 ![]() ,利用周期公式算出ω=1,得函数解析式为
,利用周期公式算出ω=1,得函数解析式为 ![]() .再由正弦函数单调区间的公式,解关于x的不等式即可得到函数f(x)的单调增区间;(II)根据函数图象平移的公式,得出函数g(x)的解析式为g(x)=2sin2x+1.由此解g(x)=0得sin2x=﹣
.再由正弦函数单调区间的公式,解关于x的不等式即可得到函数f(x)的单调增区间;(II)根据函数图象平移的公式,得出函数g(x)的解析式为g(x)=2sin2x+1.由此解g(x)=0得sin2x=﹣ ![]() ,利用正弦函数的图象解出
,利用正弦函数的图象解出 ![]() 或
或 ![]() ,可见g(x)在每个周期上恰有两个零点,若g(x)在[0,b]上至少含有10个零点,则b大于或等于g(x)在原点右侧的第10个零点,由此即可算出b的最小值.
,可见g(x)在每个周期上恰有两个零点,若g(x)在[0,b]上至少含有10个零点,则b大于或等于g(x)在原点右侧的第10个零点,由此即可算出b的最小值.
【考点精析】通过灵活运用两角和与差的正弦公式和正弦函数的单调性,掌握两角和与差的正弦公式:![]() ;正弦函数的单调性:在
;正弦函数的单调性:在![]()
![]() 上是增函数;在
上是增函数;在![]()
![]() 上是减函数即可以解答此题.
上是减函数即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,若A,B,C成等差数列,2a,2b,2c成等比数列,则sinAcosBsinC=( )
A.
B.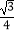
C.
D.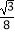
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 +y2=1(m>1)和双曲线
+y2=1(m>1)和双曲线  ﹣y2=1(n>0)有相同的焦点F1 , F2 , P是它们的一个交点,则△F1PF2的形状是( )
﹣y2=1(n>0)有相同的焦点F1 , F2 , P是它们的一个交点,则△F1PF2的形状是( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.随m,n的变化而变化 -
科目: 来源: 题型:
查看答案和解析>>【题目】在等差数列{an}中,a2+a7=﹣23,a3+a8=﹣29. (Ⅰ)求数列{an}的通项公式;
(Ⅱ)设数列{an+bn}是首项为1,公比为c的等比数列,求{bn}的前n项和Sn . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C的焦点分别为F1(﹣2
 ,0)和F2(2
,0)和F2(2  ,0),长轴长为6,设直线y=x+2交椭圆C于A、B两点.求:线段AB的中点坐标.
,0),长轴长为6,设直线y=x+2交椭圆C于A、B两点.求:线段AB的中点坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】在四棱锥P﹣ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,点E是PC的中点,作EF⊥PB交PB于点F.
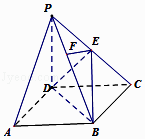
(1)求证PA∥平面EDB;
(2)求二面角C﹣PB﹣D的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知OPQ是半径为
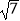 圆心角为
圆心角为  的扇形,C是该扇形弧上的动点,ABCD是扇形的内接矩形,记∠BOC为α.
的扇形,C是该扇形弧上的动点,ABCD是扇形的内接矩形,记∠BOC为α. 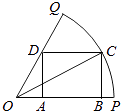
(Ⅰ)若Rt△CBO的周长为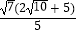 ,求
,求 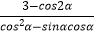 的值.
的值.
(Ⅱ)求 的最大值,并求此时α的值.
的最大值,并求此时α的值.
相关试题

