【题目】如图,已知OPQ是半径为 ![]() 圆心角为
圆心角为 ![]() 的扇形,C是该扇形弧上的动点,ABCD是扇形的内接矩形,记∠BOC为α.
的扇形,C是该扇形弧上的动点,ABCD是扇形的内接矩形,记∠BOC为α. 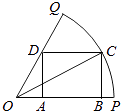
(Ⅰ)若Rt△CBO的周长为 ![]() ,求
,求 ![]() 的值.
的值.
(Ⅱ)求 ![]() 的最大值,并求此时α的值.
的最大值,并求此时α的值.
参考答案:
【答案】解:(Ⅰ)BC=OCsinα= ![]() sinα,OB=OCcosα=
sinα,OB=OCcosα= ![]() cosα,
cosα,
则若Rt△CBO的周长为  ,
,
则 ![]() +
+ ![]() sinα+
sinα+ ![]() cosα=
cosα=  ,
,
sinα+cosα= ![]() ,
,
平方得2sinαcosα= ![]() ,
,
即 ![]() =
= ![]() =
= ![]() ,
,
解得tanα=3(舍)或tanα= ![]() .
.
则 ![]() =
= ![]() =
= ![]() =
= 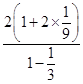 =
= ![]() .
.
(Ⅱ)在Rt△OBC中,BC=OCsinα= ![]() sinα,OB=OCcosα=
sinα,OB=OCcosα= ![]() cosα,
cosα,
在Rt△ODA中,
OA=DAtan ![]() =
= ![]() BC=
BC= ![]() sinα,
sinα,
∴AB=OB﹣OA= ![]() (cosα﹣
(cosα﹣ ![]() cosα),
cosα),
则 ![]() =|
=| ![]() |
| ![]() |=
|= ![]() (cosα﹣
(cosα﹣ ![]() cosα)
cosα) ![]() sinα
sinα ![]()
= 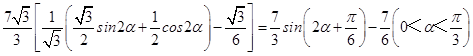
∵ ![]() ,
,
∴ ![]() ,
,
∴当 ![]() ,
,
即 ![]() 时,
时, ![]() 有最大值
有最大值 ![]() .
.
【解析】(Ⅰ)由条件利用直角三角形中的边角关系求出三角形的周长,利用三角函数的倍角公式进行化简进行求解.(Ⅱ)结合向量的数量积公式,结合三角函数的带动下进行求解.
【考点精析】本题主要考查了扇形面积公式的相关知识点,需要掌握若扇形的圆心角为![]() ,半径为
,半径为![]() ,弧长为
,弧长为![]() ,周长为
,周长为![]() ,面积为
,面积为![]() ,则
,则![]() ,
,![]() ,
,![]() 才能正确解答此题.
才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=2sinωxcosωx+2
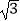 sin2ωx﹣
sin2ωx﹣ 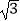 (ω>0)的最小正周期为π. (Ⅰ)求函数f(x)的单调增区间;
(ω>0)的最小正周期为π. (Ⅰ)求函数f(x)的单调增区间;
(Ⅱ)将函数f(x)的图象向左平移 个单位,再向上平移1个单位,得到函数y=g(x)的图象.若y=g(x)在[0,b](b>0)上至少含有10个零点,求b的最小值.
个单位,再向上平移1个单位,得到函数y=g(x)的图象.若y=g(x)在[0,b](b>0)上至少含有10个零点,求b的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C的焦点分别为F1(﹣2
 ,0)和F2(2
,0)和F2(2  ,0),长轴长为6,设直线y=x+2交椭圆C于A、B两点.求:线段AB的中点坐标.
,0),长轴长为6,设直线y=x+2交椭圆C于A、B两点.求:线段AB的中点坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】在四棱锥P﹣ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,点E是PC的中点,作EF⊥PB交PB于点F.
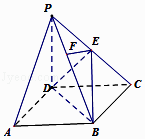
(1)求证PA∥平面EDB;
(2)求二面角C﹣PB﹣D的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】设
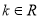 ,函数
,函数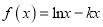 .
.(1)若
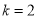 ,求曲线
,求曲线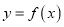 在
在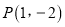 处的切线方程;
处的切线方程;(2)若
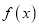 无零点,求实数
无零点,求实数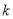 的取值范围;
的取值范围;(3)若
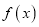 有两个相异零点
有两个相异零点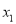 ,
, 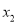 ,求证:
,求证: 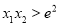
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数
 的图象,经过下列哪个平移变换,可以得到函数y=5sin2x的图象?( )
的图象,经过下列哪个平移变换,可以得到函数y=5sin2x的图象?( )
A.向右平移
B.向左平移
C.向右平移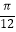
D.向左平移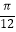
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
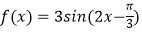 的图象为C,则如下结论中正确的是(写出所有正确结论的编号).
的图象为C,则如下结论中正确的是(写出所有正确结论的编号).
①图象C关于直线 对称;
对称;
②图象C关于点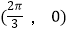 对称;
对称;
③函数f(x)在区间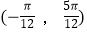 内是减函数;
内是减函数;
④把函数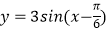 的图象上点的横坐标压缩为原来的一半(纵坐标不变)可以得到图象C.
的图象上点的横坐标压缩为原来的一半(纵坐标不变)可以得到图象C.
相关试题

