【题目】在四棱锥P﹣ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,点E是PC的中点,作EF⊥PB交PB于点F. 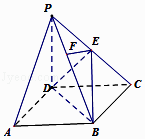
(1)求证PA∥平面EDB;
(2)求二面角C﹣PB﹣D的大小.
参考答案:
【答案】
(1)证明:连结AC,BD,交于点O,连结OE,
∵底面ABCD是正方形,∴O是AC的中点,
∵点E是PC的中点,∴OE∥PA,
∵OE平面EBD,PA平面EBD,
∴PA∥平面EDB
(2)解:以D为原点,DA,DC,DP为x,y,z轴,建立空间直角坐标系,
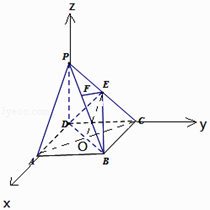
设PD=DC=1,则D(0,0,0),P(0,0,1),
B(1,1,0),C(0,1,0),
![]() =(0,0,1),
=(0,0,1), ![]() =(1,1,0),
=(1,1,0), ![]() =(0,1,﹣1),
=(0,1,﹣1),
![]() =(1,1,﹣1),
=(1,1,﹣1),
设平面PBC的法向量 ![]() =(x,y,z),平面PBD的法向量
=(x,y,z),平面PBD的法向量 ![]() =(a,b,c),
=(a,b,c),
则  ,取y=1,得
,取y=1,得 ![]() =(0,1,1),
=(0,1,1),
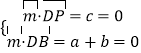 ,取a=1,得
,取a=1,得 ![]() =(1,﹣1,0),
=(1,﹣1,0),
设二面角C﹣PB﹣D的大小为θ,
则cosθ= ![]() =
= ![]() =
= ![]() ,
,
∴θ=60°,
∴二面角C﹣PB﹣D的大小为60°.
【解析】(1)连结AC,BD,交于点O,连结OE,则OE∥PA,由此能证明PA∥平面EDB.(2)以D为原点,DA,DC,DP为x,y,z轴,建立空间直角坐标系,利用向量法能求出二面角C﹣PB﹣D的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在等差数列{an}中,a2+a7=﹣23,a3+a8=﹣29. (Ⅰ)求数列{an}的通项公式;
(Ⅱ)设数列{an+bn}是首项为1,公比为c的等比数列,求{bn}的前n项和Sn . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=2sinωxcosωx+2
 sin2ωx﹣
sin2ωx﹣ 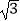 (ω>0)的最小正周期为π. (Ⅰ)求函数f(x)的单调增区间;
(ω>0)的最小正周期为π. (Ⅰ)求函数f(x)的单调增区间;
(Ⅱ)将函数f(x)的图象向左平移 个单位,再向上平移1个单位,得到函数y=g(x)的图象.若y=g(x)在[0,b](b>0)上至少含有10个零点,求b的最小值.
个单位,再向上平移1个单位,得到函数y=g(x)的图象.若y=g(x)在[0,b](b>0)上至少含有10个零点,求b的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C的焦点分别为F1(﹣2
 ,0)和F2(2
,0)和F2(2  ,0),长轴长为6,设直线y=x+2交椭圆C于A、B两点.求:线段AB的中点坐标.
,0),长轴长为6,设直线y=x+2交椭圆C于A、B两点.求:线段AB的中点坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知OPQ是半径为
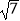 圆心角为
圆心角为  的扇形,C是该扇形弧上的动点,ABCD是扇形的内接矩形,记∠BOC为α.
的扇形,C是该扇形弧上的动点,ABCD是扇形的内接矩形,记∠BOC为α. 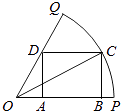
(Ⅰ)若Rt△CBO的周长为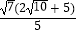 ,求
,求 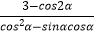 的值.
的值.
(Ⅱ)求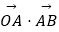 的最大值,并求此时α的值.
的最大值,并求此时α的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设
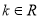 ,函数
,函数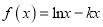 .
.(1)若
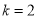 ,求曲线
,求曲线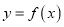 在
在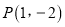 处的切线方程;
处的切线方程;(2)若
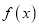 无零点,求实数
无零点,求实数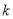 的取值范围;
的取值范围;(3)若
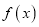 有两个相异零点
有两个相异零点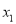 ,
, 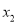 ,求证:
,求证: 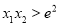
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数
 的图象,经过下列哪个平移变换,可以得到函数y=5sin2x的图象?( )
的图象,经过下列哪个平移变换,可以得到函数y=5sin2x的图象?( )
A.向右平移
B.向左平移
C.向右平移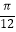
D.向左平移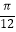
相关试题

