搜索
【题目】在△ABC中，角A，B，C所对的边分别为a，b，c，若A，B，C成等差数列，2a，2b，2c成等比数列，则sinAcosBsinC=（ ）
A.
B.
C.
D.
参考答案：
【答案】C
【解析】解：由A，B，C成等差数列，有2B=A+C，（1） ∵A，B，C为△ABC的内角，∴A+B+C=π，（2）．
由（1）（2）得B 
．
由2a，2b，2c成等比数列，得b2=ac，
由余弦定理得，b2=a2+c2﹣2accosB，
把B= 、b2=ac代入得，a2+c2﹣ac=ac，
即（a﹣c）2=0，则a=c，从而A=C=B ，
∴sinAcosBsinC= 
= 
．
故选：C．
【考点精析】本题主要考查了正弦定理的定义的相关知识点，需要掌握正弦定理:
才能正确解答此题．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知抛物线y2=2px（p＞0）的焦点为F与椭圆C的一个焦点重合，且抛物线的准线与椭圆C相交于点
． 
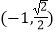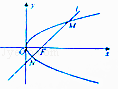
（1）求抛物线的方程；
（2）过点F是否存在直线l与椭圆C交于M，N两点，且以MN为对角线的正方形的第三个顶点恰在y轴上？若存在，求出直线l的方程；若不存在，请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数f（x）=Asin（ωx+φ），（x∈R，A＞0，ω＞0，|φ|＜
）的部分图象如图所示：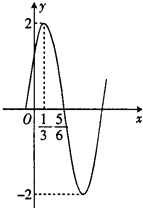 
（1）试确定f（x）的解析式；
（2）若f（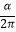
）= 
，求 
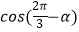的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】以下四个命题中，其中正确的个数为（ ） ①命题“若x2﹣3x+2=0，则x=1”的逆否命题为“若x≠1，则x2﹣3x+2=0”；
②“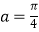
”是“cos2α=0”的充分不必要条件；
③若命题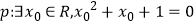
，则p：x∈R，x2+x+1=0；
④若p∧q为假，p∨q为真，则p，q有且仅有一个是真命题．
A.1
B.2
C.3
D.4 -
科目： 来源： 题型：
查看答案和解析>>【题目】已知椭圆
+y2=1（m＞1）和双曲线 
﹣y2=1（n＞0）有相同的焦点F1 ， F2 ， P是它们的一个交点，则△F1PF2的形状是（ ）
A.锐角三角形
B.直角三角形
C.钝角三角形
D.随m，n的变化而变化 -
科目： 来源： 题型：
查看答案和解析>>【题目】在等差数列{an}中，a2+a7=﹣23，a3+a8=﹣29． （Ⅰ）求数列{an}的通项公式；
（Ⅱ）设数列{an+bn}是首项为1，公比为c的等比数列，求{bn}的前n项和Sn ． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数f（x）=2sinωxcosωx+2
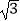sin2ωx﹣ 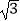（ω＞0）的最小正周期为π． （Ⅰ）求函数f（x）的单调增区间；
（Ⅱ）将函数f（x）的图象向左平移
个单位，再向上平移1个单位，得到函数y=g（x）的图象．若y=g（x）在[0，b]（b＞0）上至少含有10个零点，求b的最小值．
相关试题
