【题目】已知函数f(x)=|x﹣1|+|x﹣a|.
(1)若a=﹣1,解不等式f(x)≥3;
(2)如果x∈R,使得f(x)<2成立,求实数a的取值范围.
参考答案:
【答案】
(1)解:若a=﹣1,f(x)≥3,
即为|x﹣1|+|x+1|≥3,
当x≤﹣1时,1﹣x﹣x﹣1≥3,即有x≤﹣ ![]() ;
;
当﹣1<x<1时,1﹣x+x+1=2≥3不成立;
当x≥1时,x﹣1+x+1=2x≥3,解得x≥ ![]() .
.
综上可得,f(x)≥3的解集为(﹣∞,﹣ ![]() ]∪[
]∪[ ![]() ,+∞)
,+∞)
(2)解:x∈R,使得f(x)<2成立,
即有2>f(x)min,
由函数f(x)=|x﹣1|+|x﹣a|≥|x﹣1﹣x+a|=|a﹣1|,
当(x﹣1)(x﹣a)≤0时,取得最小值|a﹣1|,
则|a﹣1|<2,
即﹣2<a﹣1<2,
解得﹣1<a<3.
则实数a的取值范围为(﹣1,3)
【解析】(1)由题意可得|x﹣1|+|x+1|≥3,讨论当x≤﹣1时,当﹣1<x<1时,当x≥1时,去掉绝对值解不等式,最后求并集;(2)由题意可得2>f(x)min , 运用绝对值不等式的性质,可得f(x)的最小值,再由绝对值不等式的解法,可得a的范围.
【考点精析】掌握绝对值不等式的解法是解答本题的根本,需要知道含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数

(1)当
 时,讨论函数
时,讨论函数 零点的个数;
零点的个数;(2)若
 ,当
,当 =1时,求证:
=1时,求证:
-
科目: 来源: 题型:
查看答案和解析>>【题目】某小学庆“六一”晚会共由6个节目组成,演出顺序有如下要求:节目
 必须排在前两位,节目
必须排在前两位,节目 不能排在第一位,节目
不能排在第一位,节目 必须排在最后一位,该台晚会节目演出顺序的编排方案共有( )
必须排在最后一位,该台晚会节目演出顺序的编排方案共有( )A. 36种 B. 42种 C. 48种 D. 54种
-
科目: 来源: 题型:
查看答案和解析>>【题目】在独立性检验中,统计量
 有三个临界值:2.706,3.841和6.635.当
有三个临界值:2.706,3.841和6.635.当 时,有90%的把握说明两个事件有关;当
时,有90%的把握说明两个事件有关;当 时,有95%的把握说明两个事件有关,当
时,有95%的把握说明两个事件有关,当 时,有99%的把握说明两个事件有关,当
时,有99%的把握说明两个事件有关,当 时,认为两个事件无关.在一项打鼾与心脏病的调查中,共调查了2000人,经计算
时,认为两个事件无关.在一项打鼾与心脏病的调查中,共调查了2000人,经计算 .根据这一数据分析,认为打鼾与患心脏病之间( )
.根据这一数据分析,认为打鼾与患心脏病之间( )A. 有95%的把握认为两者有关 B. 约95%的打鼾者患心脏病
C. 有99%的把握认为两者有关 D. 约99%的打鼾者患心脏病
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥PABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.
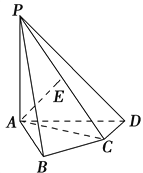
(1)证明:AE⊥平面PCD;
(2)求二面角A-PD-C的正弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△
 中,已知
中,已知 ,直线
,直线 经过点
经过点 .
.(Ⅰ)若直线
 :
: 与线段
与线段 交于点
交于点 ,且
,且 为△
为△ 的外心,求△
的外心,求△ 的外接圆的方程;
的外接圆的方程;(Ⅱ)若直线
 方程为
方程为 ,且△
,且△ 的面积为
的面积为 ,求点
,求点 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了分析本校高中生的性别与是否喜欢数学之间的关系,在高中生中随机地抽取了90名学生调查,得到了如下列联表:
喜欢数学
不喜欢数学
总计
男
30
①
45
女
②
25
45
总计
③
④
90
(1)求①②③④处分别对应的值;
(2)能有多大把握认为“高中生的性别与喜欢数学”有关?
附:

0.15
0.10
0.05
0.025
0.010
0.005
0.001

2.072
2.706
3.841
5.024
6.635
7.879
10.828
 .
.
相关试题

