【题目】根据以往的经验,某工程施工期间的降水量![]() (单位:
(单位:![]() )对工期的影响如下表:
)对工期的影响如下表:
降水量 |
|
|
|
|
工期延误天数 | 0 | 2 | 6 | 10 |
历年气象资料表明,该工程施工期间降水量![]() 小于300,700,900的概率分别为0.3,0.7,0.9,求:
小于300,700,900的概率分别为0.3,0.7,0.9,求:
(1)工期延误天数![]() 的均值与方差;
的均值与方差;
(2)在降水量![]() 至少是300的条件下,工期延误不超过6天的概率.
至少是300的条件下,工期延误不超过6天的概率.
参考答案:
【答案】(1)![]() ;
;![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)由题意,该工程施工期间降水![]() 小于
小于![]() 的概率分别为
的概率分别为![]() ,结合工程施工期间的降水量对工期的影响,可求相应的概率,金额可得延误天数
,结合工程施工期间的降水量对工期的影响,可求相应的概率,金额可得延误天数![]() 的均值与方差;(2)利用概率的加法公式,可得各个概率值,再利用条件概率,即可得到结论.
的均值与方差;(2)利用概率的加法公式,可得各个概率值,再利用条件概率,即可得到结论.
试题解析:(1)由已知条件和概率的加法公式,有
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
所以![]() 的分布列为:
的分布列为:
| 0 | 2 | 6 | 10 |
| 0.3 | 0.4 | 0.2 | 0.1 |
于是,![]() ;
;
D(Y)=(0-3)2×0.3+(2-3)2×0.4+(6-3)2×0.2+(10-3)2×0.1=9.8.
故工期延误天数Y的均值为3,方差为9.8,
(2)由概率的加法公式,![]() ,
,
又![]() .
.
由条件概率,得
![]() .
.
故在降水量![]() 至少是300
至少是300![]() 的条件下,工期延期不超过6天的概率是
的条件下,工期延期不超过6天的概率是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某上市股票在30天内每股的交易价格
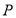 (元)与时间
(元)与时间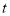 (天)组成有序数对
(天)组成有序数对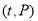 ,点
,点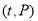 落在图中的两条线段上.
落在图中的两条线段上.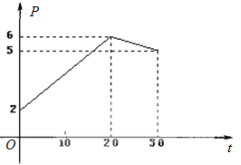
该股票在30天内的日交易量
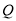 (万股)与时间
(万股)与时间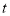 (天)的部分数据如下表所示:
(天)的部分数据如下表所示:第
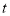 天
天4
10
16
22
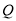 (万股)
(万股)36
30
24
18
(1)根据提供的图象,写出该股票每股交易价格
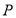 (元)与时间
(元)与时间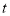 (天)所满足的函数关系式;
(天)所满足的函数关系式;(2)根据表中数据,写出日交易量
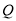 (万股)与时间
(万股)与时间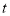 (天)的一次函数关系式;
(天)的一次函数关系式;(3)用
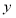 (万元)表示该股票日交易额,写出
(万元)表示该股票日交易额,写出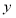 关于
关于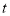 的函数关系式,并求在这30天内第几天日交易额最大,最大值为多少?
的函数关系式,并求在这30天内第几天日交易额最大,最大值为多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
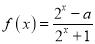 (
(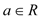 )的图像关于坐标原点对称。
)的图像关于坐标原点对称。(1)求
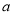 的值,并求出函数
的值,并求出函数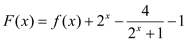 的零点;
的零点;(2)若函数
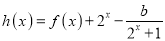 在
在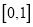 内存在零点,求实数
内存在零点,求实数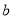 的取值范围;
的取值范围;(3)设
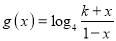 ,若不等式
,若不等式 在
在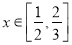 上恒成立,求满足条件的最小整数
上恒成立,求满足条件的最小整数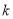 的值。
的值。 -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人练习罚球,每人练习6组,每组罚球20个,命中个数茎叶图如下:
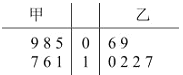
(1)求甲命中个数的中位数和乙命中个数的众数;
(2)通过计算,比较甲乙两人的罚球水平.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某医药研究所开发一种新药,在试验药效时发现:如果成人按规定剂量服用,那么服药后每毫升血液中的含药量y(微克)与时间x(小时)之间满足y=
 其对应曲线(如图所示)过点
其对应曲线(如图所示)过点 .
. 
(1)试求药量峰值(y的最大值)与达峰时间(y取最大值时对应的x值);
(2)如果每毫升血液中含药量不少于1微克时治疗疾病有效,那么成人按规定剂量服用该药后一次能维持多长的有效时间(精确到0.01小时)?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 ,
,  。
。(1)写出
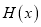 的解析式与定义域;
的解析式与定义域;(2)画出函数
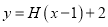 的图像;
的图像;(3)试讨论方程
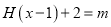 的根的个数。
的根的个数。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
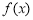 是单调减函数,若将方程
是单调减函数,若将方程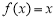 与
与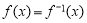 的解分别称为函数
的解分别称为函数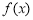 的不动点与稳定点.则“
的不动点与稳定点.则“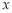 是
是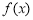 的不动点”是“
的不动点”是“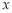 是
是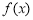 的稳定点”的 ( )
的稳定点”的 ( )A.充要条件 B.充分不必要条件
C.必要不充分条件 D.既不充分也不必要条件
相关试题

