【题目】已知![]() 是单调减函数,若将方程
是单调减函数,若将方程![]() 与
与![]() 的解分别称为函数
的解分别称为函数![]() 的不动点与稳定点.则“
的不动点与稳定点.则“![]() 是
是![]() 的不动点”是“
的不动点”是“![]() 是
是![]() 的稳定点”的 ( )
的稳定点”的 ( )
A.充要条件 B.充分不必要条件
C.必要不充分条件 D.既不充分也不必要条件
参考答案:
【答案】B
【解析】欲判断”x是f(x)的不动点”是“x是f(x)的稳定点”的什么条件,只须从两个方面考虑:一方面:若x是f(x)的不动点,看能不能推出“x是f(x)的稳定点“;另一方面:”x是f(x)的稳定点“能不能推出“x是f(x)的不动点“.
解:一方面:若x是f(x)的不动点,
则f(x)=x,即函数y=f(x)与直线y=x的交点的横坐标为x,
因为原函数与反函数的图象一定要关于直线y=x对称,
故反函数的图象一定要过函数y=f(x)与直线y=x的横坐标为x交点,
即f(x)=f-1(x)的解是x,
故”x是f(x)的不动点“x是f(x)的稳定点“;
另一方面:x是f(x)的稳定点,
即f(x)=f-1(x),即函数y=f(x)与y=f-1(x)的交点的横坐标为x,
因为原函数与反函数的图象的交点不一定在直线y=x上,
故原函数的图象不一定要过函数y=f(x)与反函数的图象的交点,
即x不一定是方程f(x)=f-1(x)的解
故”x是f(x)的稳定点“不能”x是f(x)的不动点“
则x“是f(x)的不动点”是“x是f(x)的稳定点”的“充分不必要条件.
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据以往的经验,某工程施工期间的降水量
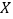 (单位:
(单位: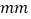 )对工期的影响如下表:
)对工期的影响如下表:降水量
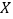
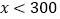
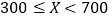
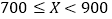
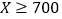
工期延误天数
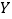
0
2
6
10
历年气象资料表明,该工程施工期间降水量
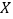 小于300,700,900的概率分别为0.3,0.7,0.9,求:
小于300,700,900的概率分别为0.3,0.7,0.9,求:(1)工期延误天数
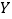 的均值与方差;
的均值与方差;(2)在降水量
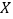 至少是300的条件下,工期延误不超过6天的概率.
至少是300的条件下,工期延误不超过6天的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】某医药研究所开发一种新药,在试验药效时发现:如果成人按规定剂量服用,那么服药后每毫升血液中的含药量y(微克)与时间x(小时)之间满足y=
 其对应曲线(如图所示)过点
其对应曲线(如图所示)过点 .
. 
(1)试求药量峰值(y的最大值)与达峰时间(y取最大值时对应的x值);
(2)如果每毫升血液中含药量不少于1微克时治疗疾病有效,那么成人按规定剂量服用该药后一次能维持多长的有效时间(精确到0.01小时)?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 ,
,  。
。(1)写出
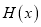 的解析式与定义域;
的解析式与定义域;(2)画出函数
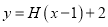 的图像;
的图像;(3)试讨论方程
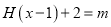 的根的个数。
的根的个数。 -
科目: 来源: 题型:
查看答案和解析>>【题目】某家庭进行理财投资,根据长期收益率市场预测,投资
 类产品的收益与投资额成正比,投资
类产品的收益与投资额成正比,投资 类产品的收益与投资额的算术平方根成正比.已知投资1万元时
类产品的收益与投资额的算术平方根成正比.已知投资1万元时 两类产品的收益分别为0.125万元和0.5万元.
两类产品的收益分别为0.125万元和0.5万元.(1)分别写出
 两类产品的收益与投资额的函数关系;
两类产品的收益与投资额的函数关系;(2)该家庭有20万元资金,全部用于理财投资,问:怎么分配资金能使投资获得最大收益,其最大收益是多少万元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】上周某校高三年级学生参加了数学测试,年部组织任课教师对这次考试进行成绩分析.现从中抽取80名学生的数学成绩(均为整数)的频率分布直方图如图所示.
(Ⅰ)估计这次月考数学成绩的平均分和众数;
(Ⅱ)假设抽出学生的数学成绩在
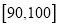 段各不相同,且都超过94分.若将频率视为概率,现用简单随机抽样的方法,从95,96,97,98,99,100这6个数字中任意抽取2个数,有放回地抽取3次,记这3次抽取中恰好有两名学生的数学成绩的次数为
段各不相同,且都超过94分.若将频率视为概率,现用简单随机抽样的方法,从95,96,97,98,99,100这6个数字中任意抽取2个数,有放回地抽取3次,记这3次抽取中恰好有两名学生的数学成绩的次数为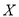 ,求
,求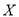 的分布列和期望.
的分布列和期望.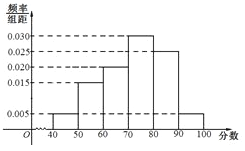
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
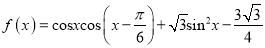 .
.(1)求
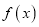 的最小正周期
的最小正周期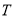 ;
;(2)设
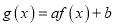 ,若
,若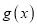 在
在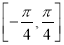 上的值域为
上的值域为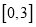 ,求实数
,求实数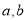 的值;
的值;(3)若
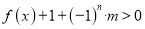 对任意的
对任意的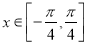 和
和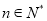 恒成立,求实数
恒成立,求实数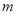 的取值范围.
的取值范围.
相关试题

