【题目】已知![]() (
(![]() )的图像关于坐标原点对称。
)的图像关于坐标原点对称。
(1)求![]() 的值,并求出函数
的值,并求出函数![]() 的零点;
的零点;
(2)若函数![]() 在
在![]() 内存在零点,求实数
内存在零点,求实数![]() 的取值范围;
的取值范围;
(3)设![]() ,若不等式
,若不等式![]() 在
在![]() 上恒成立,求满足条件的最小整数
上恒成立,求满足条件的最小整数![]() 的值。
的值。
参考答案:
【答案】(1) ![]() ,
, ![]() 的零点为
的零点为![]() ;(2)
;(2)![]() ;(3)最小整数
;(3)最小整数![]() 的值是
的值是![]() .
.
【解析】试题分析:(1)由题意知f(x)是R上的奇函数,由f(0)=0,得a=1,即可求出F(x)的表达式,令F(x)=0解得![]() =0,此方程可视为“
=0,此方程可视为“![]() ”的二次方程,解之即可.
”的二次方程,解之即可.
(2)由题设知h(x)=0在[0,1]内有解,即方程![]() 在[0,1]内有解.分离变量,利用指数函数和二次函数的单调性即可得出.
在[0,1]内有解.分离变量,利用指数函数和二次函数的单调性即可得出.
(3)由![]() ,得
,得![]() ,变量分离可得
,变量分离可得![]() ,然后通过换元、利用基本不等式的性质即可得出.
,然后通过换元、利用基本不等式的性质即可得出.
试题解析:
(1)由题意知![]() 是R上的奇函数,所以
是R上的奇函数,所以![]() ,得
,得![]() 。
。
![]() ,
, ![]() =
=![]() +
+![]() =
= ,
,
由![]() =0,可得
=0,可得![]() =2,所以,
=2,所以, ![]() ,即
,即![]() 的零点为
的零点为![]() 。
。
(2) ,
,
有题设知![]() 在
在![]() 内有解,即方程
内有解,即方程![]() 在
在![]() 内有解。
内有解。
![]() 在
在![]() 内递增,得
内递增,得![]() 。
。
所以当![]() 时,函数
时,函数![]() 在
在![]() 内存在零点。
内存在零点。
(3)由![]() ,得
,得![]() ,
,
![]() ,显然
,显然![]() 时
时![]() ,即
,即![]() 。
。
设![]() ,
,
于是![]() ,所以
,所以![]() 。
。
满足条件的最小整数![]() 的值是
的值是![]() 。
。
-
科目: 来源: 题型:
查看答案和解析>>【题目】在高中学习过程中,同学们经常这样说:“如果物理成绩好,那么学习数学就没什么问题.”某班针对“高中生物理学习对数学学习的影响”进行研究,得到了学生的物理成绩与数学成绩具有线性相关关系的结论.现从该班随机抽取5名学生在一次考试中的物理和数学成绩,如下表:
编号
成绩
1
2
3
4
5
物理(
 )
)90
85
74
68
63
数学(
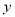 )
)130
125
110
95
90
求数学成绩
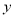 关于物理成绩
关于物理成绩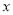 的线性回归方程
的线性回归方程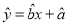 (
(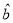 精确到
精确到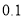
若某位学生的物理成绩为80分,预测他的数学成绩;
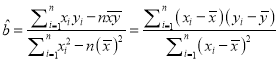
-
科目: 来源: 题型:
查看答案和解析>>【题目】某企业接到生产3000台某产品的A,B,C三种部件的订单,每台产品需要这三种部件的数量分别为2,2,1(单位:件).已知每个工人每天可生产A部件6件,或B部件3件,或C部件2件.该企业计划安排200名工人分成三组分别生产这三种部件,生产B部件的人数与生产A部件的人数成正比,比例系数为k(k为正整数).
(1)设生产A部件的人数为x,分别写出完成A,B,C三种部件生产需要的时间;
(2)假设这三种部件的生产同时开工,试确定正整数k的值,使完成订单任务的时间最短,并给出时间最短时具体的人数分组方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某上市股票在30天内每股的交易价格
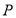 (元)与时间
(元)与时间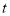 (天)组成有序数对
(天)组成有序数对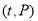 ,点
,点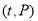 落在图中的两条线段上.
落在图中的两条线段上.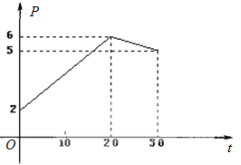
该股票在30天内的日交易量
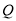 (万股)与时间
(万股)与时间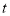 (天)的部分数据如下表所示:
(天)的部分数据如下表所示:第
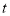 天
天4
10
16
22
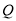 (万股)
(万股)36
30
24
18
(1)根据提供的图象,写出该股票每股交易价格
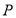 (元)与时间
(元)与时间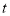 (天)所满足的函数关系式;
(天)所满足的函数关系式;(2)根据表中数据,写出日交易量
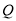 (万股)与时间
(万股)与时间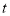 (天)的一次函数关系式;
(天)的一次函数关系式;(3)用
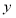 (万元)表示该股票日交易额,写出
(万元)表示该股票日交易额,写出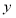 关于
关于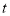 的函数关系式,并求在这30天内第几天日交易额最大,最大值为多少?
的函数关系式,并求在这30天内第几天日交易额最大,最大值为多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人练习罚球,每人练习6组,每组罚球20个,命中个数茎叶图如下:
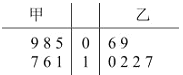
(1)求甲命中个数的中位数和乙命中个数的众数;
(2)通过计算,比较甲乙两人的罚球水平.
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据以往的经验,某工程施工期间的降水量
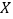 (单位:
(单位: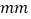 )对工期的影响如下表:
)对工期的影响如下表:降水量
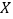
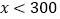
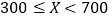
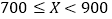
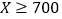
工期延误天数
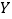
0
2
6
10
历年气象资料表明,该工程施工期间降水量
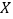 小于300,700,900的概率分别为0.3,0.7,0.9,求:
小于300,700,900的概率分别为0.3,0.7,0.9,求:(1)工期延误天数
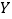 的均值与方差;
的均值与方差;(2)在降水量
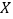 至少是300的条件下,工期延误不超过6天的概率.
至少是300的条件下,工期延误不超过6天的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】某医药研究所开发一种新药,在试验药效时发现:如果成人按规定剂量服用,那么服药后每毫升血液中的含药量y(微克)与时间x(小时)之间满足y=
 其对应曲线(如图所示)过点
其对应曲线(如图所示)过点 .
. 
(1)试求药量峰值(y的最大值)与达峰时间(y取最大值时对应的x值);
(2)如果每毫升血液中含药量不少于1微克时治疗疾病有效,那么成人按规定剂量服用该药后一次能维持多长的有效时间(精确到0.01小时)?
相关试题

