【题目】(本小题满分12分)
如图在直三棱柱ABC—A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的
中点.
(1) 求证: AC⊥BC1
(2) 求证:AC1∥平面CDB1
(3) 求异面直线AC1与B1C所成角的余弦值.
参考答案:
【答案】![]()
【解析】
试题分析:(1)由勾股定理计算得AC⊥BC,再由直棱柱性质得C1C⊥AC,最后根据线面垂直判定定理得AC⊥平面BCC1B1,即得AC⊥BC1.(2)设CB1与C1B的交点为E,由三角形中位线性质得DE∥AC1,再根据线面平行判定定理得结论(3)因为DE∥AC1,所以∠CED为AC1与B1C所成的角.再根据解三角形得所成角的余弦值.
试题解析:(1)证明:在直三棱柱ABC-A1B1C1中,底面三边长AC=3,BC=4,AB=5,∴AC⊥BC.
又∵C1C⊥AC.∴AC⊥平面BCC1B1.
∵BC1平面BCC1B,∴AC⊥BC1.
(2)证明:设CB1与C1B的交点为E,连接DE,又四边形BCC1B1为正方形.
∵D是AB的中点,E是BC1的中点,∴DE∥AC1.
∵DE平面CDB1,AC1平面CDB1,
∴AC1∥平面CDB1.
(3)∵DE∥AC1,
∴∠CED为AC1与B1C所成的角.在△CED中,ED=![]() AC1=
AC1=![]() ,
,
CD=![]() AB=
AB=![]() ,CE=
,CE=![]() CB1=2
CB1=2![]() ,∴cos∠CED=
,∴cos∠CED=![]() =
=![]() .
.
∴异面直线AC1与B1C所成角的余弦值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设

 是等差数列,
是等差数列, 是其前
是其前 项的和,且
项的和,且 ,则下列结论错误的是( )
,则下列结论错误的是( )A.
 B.
B.  C.
C.  D.
D.  与
与 均为
均为 的最大值
的最大值 -
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)=lnx+
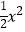 +ax(a∈R),g(x)=ex+
+ax(a∈R),g(x)=ex+ 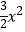 .
.
(1)讨论f(x)的极值点的个数;
(2)若对于x>0,总有f(x)≤g(x).(i)求实数a的取值范围;(ii)求证:对于x>0,不等式ex+x2﹣(e+1)x+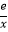 >2成立.
>2成立. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,在区间
,在区间 内任取两个实数
内任取两个实数 ,
, ,且
,且 ,若不等式
,若不等式 恒成立,则实数
恒成立,则实数 的取值范围是
的取值范围是A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
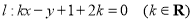 .
.(1)若直线
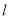 不经过第四象限,求
不经过第四象限,求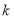 的取值范围;
的取值范围;(2)若直线
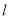 交
交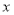 轴负半轴于点
轴负半轴于点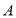 ,交
,交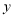 轴正半轴于点
轴正半轴于点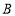 ,
, 为坐标原点,设
为坐标原点,设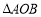 的面积为
的面积为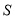 ,求
,求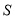 的最小值及此时直线
的最小值及此时直线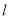 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系中,以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系.已知点M的极坐标为
 ,圆C的参数方程为
,圆C的参数方程为  (α为参数).
(α为参数).
(1)直线l过M且与圆C相切,求直线l的极坐标方程;
(2)过点P(0,m)且斜率为 的直线l'与圆C交于A,B两点,若|PA||PB|=6,求实数m的值.
的直线l'与圆C交于A,B两点,若|PA||PB|=6,求实数m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
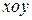 中,
中,
已知圆
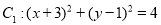 和圆
和圆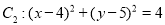 .
.(1)若直线
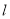 过点
过点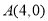 ,且被圆
,且被圆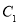 截得的弦长为
截得的弦长为 ,
,求直线
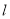 的方程;(2)设P为平面上的点,满足:
的方程;(2)设P为平面上的点,满足:存在过点P的无穷多对互相垂直的直线
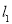 和
和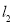 ,
,它们分别与圆
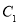 和圆
和圆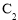 相交,且直线
相交,且直线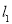 被圆
被圆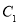
截得的弦长与直线
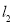 被圆
被圆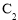 截得的弦长相等,试求所有满足条件的点P的坐标。
截得的弦长相等,试求所有满足条件的点P的坐标。
相关试题

