【题目】已知直线![]() .
.
(1)若直线![]() 不经过第四象限,求
不经过第四象限,求![]() 的取值范围;
的取值范围;
(2)若直线![]() 交
交![]() 轴负半轴于点
轴负半轴于点![]() ,交
,交![]() 轴正半轴于点
轴正半轴于点![]() ,
,![]() 为坐标原点,设
为坐标原点,设![]() 的面积为
的面积为![]() ,求
,求![]() 的最小值及此时直线
的最小值及此时直线![]() 的方程.
的方程.
参考答案:
【答案】(1)k≥0;(2)面积最小值为4,此时直线方程为:x﹣2y+4=0
【解析】
(1)可求得直线l的方程及直线l在y轴上的截距,依题意,![]() 从而可解得k的取值范围;
从而可解得k的取值范围;
(2)依题意可求得A(﹣![]() ,0),B(0,1+2k),S=
,0),B(0,1+2k),S=![]() (4k+
(4k+![]() +4),利用基本不等式即可求得答案.
+4),利用基本不等式即可求得答案.
(1)直线l的方程可化为:y=kx+2k+1,则直线l在y轴上的截距为2k+1,
要使直线l不经过第四象限,则![]() ,解得k的取值范围是:k≥0
,解得k的取值范围是:k≥0
(2)依题意,直线l在x轴上的截距为:﹣![]() ,在y轴上的截距为1+2k,
,在y轴上的截距为1+2k,
∴A(﹣![]() ,0),B(0,1+2k),又﹣
,0),B(0,1+2k),又﹣![]() <0且1+2k>0,
<0且1+2k>0,
∴k>0,故S=![]() |OA||OB|=
|OA||OB|=![]() ×
×![]() (1+2k)=
(1+2k)=![]() (4k+
(4k+![]() +4)≥
+4)≥![]() (4+4)=4,当且仅当4k=
(4+4)=4,当且仅当4k=![]() ,即k=
,即k=![]() 时取等号,
时取等号,
故S的最小值为4,此时直线l的方程为x﹣2y+4=0
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
 .
.(1)若直线
 不经过第四象限,求
不经过第四象限,求 的取值范围;
的取值范围;(2)若直线
 交
交 轴负半轴于点
轴负半轴于点 ,交
,交 轴正半轴于点
轴正半轴于点 ,
, 为坐标原点,设
为坐标原点,设 的面积为
的面积为 ,求
,求 的最小值及此时直线
的最小值及此时直线 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
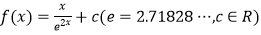 .
.
(1)求f(x)的单调区间及最大值;
(2)讨论关于x的方程|lnx|=f(x)根的个数. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分12分)
围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:元)。

(Ⅰ)将y表示为x的函数;
(Ⅱ)试确定x,使修建此矩形场地围墙的总费用最小,并求出最小总费用。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为研究学生的身体素质与课外体育锻炼时间的关系,对该校200名高三学生平均每天课外体育锻炼时间进行调查,如表:(平均每天锻炼的时间单位:分钟)
平均每天锻炼的时间/分钟





总人数
20
36
44
50
40
10
将学生日均课外体育锻炼时间在
 的学生评价为“课外体育达标”.
的学生评价为“课外体育达标”.(1)请根据上述表格中的统计数据填写下面的
 列联表;
列联表;课外体育不达标
课外体育达标
合计
男
女
20
110
合计
(2)通过计算判断是否能在犯错误的概率不超过
 的前提下认为“课外体育达标”性别有关?
的前提下认为“课外体育达标”性别有关?参考公式
 ,其中
,其中

0.25
0.15
0.10
0.05
0.025
0.010
0.005
0.001

1.323
2.072
2.706
3.841
5.024
6.635
7.879
10.828
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
 满足:
满足:  ,且
,且 .
.(1)求证:数列
 是等比数列;
是等比数列;(2)设
 是数列
是数列 的前
的前 项和,若
项和,若 对任意
对任意 都成立.试求
都成立.试求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】交强险是车主必须为机动车购买的险种,若普通6座以下私家车投保交强险第一年的费用(基准保费)统一为
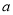 元,在下一年续保时,实行的是费率浮动机制,保费与上一年度车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就是越高,具体浮动情况如下表:
元,在下一年续保时,实行的是费率浮动机制,保费与上一年度车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就是越高,具体浮动情况如下表:交强险浮动因素和浮动费率比率表
浮动因素
浮动比率
上一个年度未发生有责任道路交通事故
下浮10%
上两个年度未发生有责任道路交通事故
下浮20%
上三个及以上年度未发生有责任道路交通事故
下浮30%
上一个年度发生一次有责任不涉及死亡的道路交通事故
0%
上一个年度发生两次及两次以上有责任道路交通事故
上浮10%
上一个年度发生有责任道路交通死亡事故
上浮30%
某机构为了 某一品牌普通6座以下私家车的投保情况,随机抽取了60辆车龄已满三年的该品牌同型号私家车的下一年续保时的情况,统计得到了下面的表格:
类型
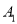
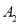
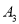
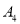
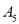
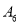
数量
10
5
5
20
15
5
以这60辆该品牌车的投保类型的频率代替一辆车投保类型的概率,完成下列问题:
(1)按照我国《机动车交通事故责任强制保险条例》汽车交强险价格的规定,
 ,记
,记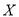 为某同学家的一辆该品牌车在第四年续保时的费用,求
为某同学家的一辆该品牌车在第四年续保时的费用,求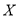 的分布列与数学期望;(数学期望值保留到个位数字)
的分布列与数学期望;(数学期望值保留到个位数字)(2)某二手车销售商专门销售这一品牌的二手车,且将下一年的交强险保费高于基本保费的车辆记为事故车,假设购进一辆事故车亏损5000元,一辆非事故车盈利10000元:
①若该销售商购进三辆(车龄已满三年)该品牌二手车,求这三辆车中至多有一辆事故车的概率;
②若该销售商一次购进100辆(车龄已满三年)该品牌二手车,求他获得利润的期望值.
相关试题

