【题目】在平面直角坐标系![]() 中,
中,
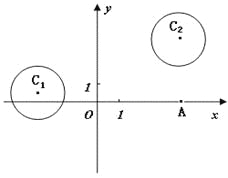
已知圆![]() 和圆
和圆![]() .
.
(1)若直线![]() 过点
过点![]() ,且被圆
,且被圆![]() 截得的弦长为
截得的弦长为![]() ,
,
求直线![]() 的方程;(2)设P为平面上的点,满足:
的方程;(2)设P为平面上的点,满足:
存在过点P的无穷多对互相垂直的直线![]() 和
和![]() ,
,
它们分别与圆![]() 和圆
和圆![]() 相交,且直线
相交,且直线![]() 被圆
被圆![]()
截得的弦长与直线![]() 被圆
被圆![]() 截得的弦长相等,试求所有满足条件的点P的坐标。
截得的弦长相等,试求所有满足条件的点P的坐标。
参考答案:
【答案】(1)![]() 或
或![]() ,(2)P在以C1C2的中垂线上,且与C1、C2等腰直角三角形,利用几何关系计算可得点P坐标为
,(2)P在以C1C2的中垂线上,且与C1、C2等腰直角三角形,利用几何关系计算可得点P坐标为![]() 或
或![]() 。
。
【解析】
(1)设直线l的方程为y=k(x-4),即kx-y-4k=0.由垂径定理,得圆心C1到直线l的距离d=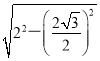 =1,结合点到直线距离公式,得
=1,结合点到直线距离公式,得![]() =1,化简得24k2+7k=0,解得k=0或k=-
=1,化简得24k2+7k=0,解得k=0或k=-![]() .
.
所求直线l的方程为y=0或y=-![]() (x-4),即y=0或7x+24y-28=0.
(x-4),即y=0或7x+24y-28=0.
(2)设点P坐标为(m,n),直线l1、l2的方程分别为y-n=k(x-m),y-n=-![]() (x-m),即kx-y+n-km=0,-
(x-m),即kx-y+n-km=0,-![]() x-y+n+
x-y+n+![]() m=0.
m=0.
因为直线l1被圆C1截得的弦长与直线l2被圆C2截得的弦长相等,两圆半径相等.由垂径定理,得圆心C1到直线l1与圆心C2到直线l2的距离相等.故有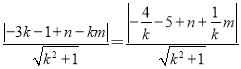 ,
,
化简得(2-m-n)k=m-n-3或(m-n+8)k=m+n-5.
因为关于k的方程有无穷多解,所以有![]()
解得点P坐标为![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分12分)
如图在直三棱柱ABC—A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的
中点.
(1) 求证: AC⊥BC1
(2) 求证:AC1∥平面CDB1
(3) 求异面直线AC1与B1C所成角的余弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
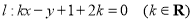 .
.(1)若直线
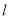 不经过第四象限,求
不经过第四象限,求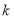 的取值范围;
的取值范围;(2)若直线
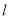 交
交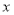 轴负半轴于点
轴负半轴于点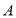 ,交
,交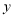 轴正半轴于点
轴正半轴于点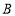 ,
, 为坐标原点,设
为坐标原点,设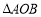 的面积为
的面积为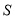 ,求
,求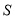 的最小值及此时直线
的最小值及此时直线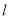 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系中,以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系.已知点M的极坐标为
 ,圆C的参数方程为
,圆C的参数方程为  (α为参数).
(α为参数).
(1)直线l过M且与圆C相切,求直线l的极坐标方程;
(2)过点P(0,m)且斜率为 的直线l'与圆C交于A,B两点,若|PA||PB|=6,求实数m的值.
的直线l'与圆C交于A,B两点,若|PA||PB|=6,求实数m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知边长为
 的正
的正 的顶点
的顶点 在平面
在平面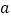 内,顶点
内,顶点 ,
, 在平面
在平面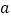 外的同一侧,点
外的同一侧,点 ,
, 分别为
分别为 ,
, 在平面
在平面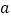 内的投影,设
内的投影,设 ,直线
,直线 与平面
与平面 所成的角为
所成的角为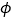 .若
.若 是以角
是以角 为直角的直角三角形,则
为直角的直角三角形,则 的最小值为__________.
的最小值为__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】下表是某地一家超市在2018年一月份某一周内周2到周6的时间
 与每天获得的利润
与每天获得的利润 (单位:万元)的有关数据.
(单位:万元)的有关数据.星期

星期2
星期3
星期4
星期5
星期6
利润

2
3
5
6
9
(1)根据上表提供的数据,用最小二乘法求线性回归直线方程
 ;
;(2)估计星期日获得的利润为多少万元.
参考公式:

-
科目: 来源: 题型:
查看答案和解析>>【题目】树立和践行“绿水青山就是金山银山,坚持人与自然和谐共生”的理念越来越深入人心,已形成了全民自觉参与,造福百姓的良性循环.据此,某网站推出了关于生态文明建设进展情况的调查,调查数据表明,环境治理和保护问题仍是百姓最为关心的热点,参与调查者中关注此问题的约占
 .现从参与关注生态文明建设的人群中随机选出200人,并将这200人按年龄分组:第1组
.现从参与关注生态文明建设的人群中随机选出200人,并将这200人按年龄分组:第1组 ,第2组
,第2组 ,第3组
,第3组 ,第4组
,第4组 ,第5组
,第5组 ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
(1)求出
 的值;
的值;(2)现在要从年龄较小的第1,2组中用分层抽样的方法抽取5人,再从这5人中随机抽取3人进行问卷调查,求第2组恰好抽到2人的概率.
相关试题

