【题目】函数f(x)=lnx+ ![]() +ax(a∈R),g(x)=ex+
+ax(a∈R),g(x)=ex+ ![]() .
.
(1)讨论f(x)的极值点的个数;
(2)若对于x>0,总有f(x)≤g(x).(i)求实数a的取值范围;(ii)求证:对于x>0,不等式ex+x2﹣(e+1)x+ ![]() >2成立.
>2成立.
参考答案:
【答案】
(1)解:由题意得f'(x)=x+ ![]() +a=
+a= ![]() ,
,
当a2﹣4≤0,即﹣2≤a≤2时,f'(x)≥0恒成立,无极值点;
当a2﹣4>0,即a<﹣2或a>2时,
①a<﹣2时,设方程x2+ax+1=0两个不同实根为x1,x2,不妨设x1<x1,x2,
则x1+x2=﹣a>0,x1x2=1>0,故0<x1<x2,
∴x1,x2是函数的两个极值点.
②a>2时,设方程x2+ax+1=0两个不同实根为x1,x2,
则x1+x2=﹣a<0,x1x2=1>0,故x1<0,x2<0,
故函数没有极值点.
综上,当a<﹣2时,函数有两个极值点;
当a≥﹣2时,函数没有极值点
(2)解:(i)f(x)≤g(x)等价于ex﹣lnx+x2≥ax,
由x>0,即a≤ ![]() 对于x>0恒成立,
对于x>0恒成立,
设φ(x)= ![]() (x>0),
(x>0),
φ′(x)= ![]() ,
,
∵x>0,∴x∈(0,1)时,φ'(x)<0,φ(x)单调递减,
x∈(1,+∞)时,φ'(x)>0,φ(x)单调递增,
∴φ(x)≥φ(1)=e+1,
∴a≤e+1.
(ii)( ii)由( i)知,当a=e+1时有f(x)≤g(x),
即:ex+ ![]() x2≥lnx+
x2≥lnx+ ![]() x2+(e+1)x,
x2+(e+1)x,
等价于ex+x2﹣(e+1)x≥lnx…①当且仅当x=1时取等号,
以下证明:lnx+ ![]() ≥2,
≥2,
设θ(x)=lnx+ ![]() ,则θ′(x)=
,则θ′(x)= ![]() ﹣
﹣ ![]() =
= ![]() ,
,
∴当x∈(0,e)时θ'(x)<0,θ(x)单调递减,
x∈(e,+∞)时θ'(x)>0,θ(x)单调递增,
∴θ(x)≥θ(e)=2,
∴lnx+ ![]() ≥2,②当且仅当x=e时取等号;
≥2,②当且仅当x=e时取等号;
由于①②等号不同时成立,故有ex+x2﹣(e+1)x+ ![]() >2
>2
【解析】(1)求f(x)的导数f′(x),根据x>0求出f'(x)的值域,讨论a的值得出f′(x)的正负情况,判断f(x)的单调性和极值点问题;(2)(i)f(x)≤g(x)等价于ex﹣lnx+x2≥ax,由x>0,利用分离常数法求出a的表达式,再构造函数求最值即可;(ii)由( i)结论,a=e+1时有f(x)≤g(x),得出不等式,再进行等价转化,证明转化的命题成立即可.
【考点精析】通过灵活运用利用导数研究函数的单调性和函数的极值与导数,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值即可以解答此题.
是极小值即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班制定了数学学习方案:星期一和星期日分别解决
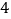 个数学问题,且从星期二开始,每天所解决问题的个数与前一天相比,要么“多一个”要么“持平”要么“少一个”,则在一周中每天所解决问题个数的不同方案共有( )
个数学问题,且从星期二开始,每天所解决问题的个数与前一天相比,要么“多一个”要么“持平”要么“少一个”,则在一周中每天所解决问题个数的不同方案共有( )A.
 种 B.
种 B. 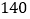 种 C.
种 C. 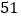 种 D.
种 D. 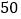 种
种 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆E:
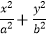 =1(a>b>0)的左、右焦点分别为F1、F2 , A为椭圆E的右顶点,B,C分别为椭圆E的上、下顶点.线段CF2的延长线与线段AB交于点M,与椭圆E交于点P.
=1(a>b>0)的左、右焦点分别为F1、F2 , A为椭圆E的右顶点,B,C分别为椭圆E的上、下顶点.线段CF2的延长线与线段AB交于点M,与椭圆E交于点P.
(1)若椭圆的离心率为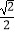 ,△PF1C的面积为12,求椭圆E的方程;
,△PF1C的面积为12,求椭圆E的方程;
(2)设S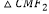 =λS
=λS 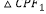 ,求实数λ的最小值.
,求实数λ的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设

 是等差数列,
是等差数列, 是其前
是其前 项的和,且
项的和,且 ,则下列结论错误的是( )
,则下列结论错误的是( )A.
 B.
B.  C.
C.  D.
D.  与
与 均为
均为 的最大值
的最大值 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,在区间
,在区间 内任取两个实数
内任取两个实数 ,
, ,且
,且 ,若不等式
,若不等式 恒成立,则实数
恒成立,则实数 的取值范围是
的取值范围是A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分12分)
如图在直三棱柱ABC—A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的
中点.
(1) 求证: AC⊥BC1
(2) 求证:AC1∥平面CDB1
(3) 求异面直线AC1与B1C所成角的余弦值.
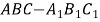
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
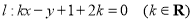 .
.(1)若直线
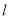 不经过第四象限,求
不经过第四象限,求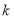 的取值范围;
的取值范围;(2)若直线
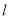 交
交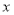 轴负半轴于点
轴负半轴于点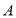 ,交
,交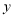 轴正半轴于点
轴正半轴于点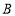 ,
, 为坐标原点,设
为坐标原点,设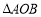 的面积为
的面积为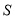 ,求
,求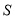 的最小值及此时直线
的最小值及此时直线 的方程.
的方程.
相关试题

