【题目】某地区100位居民的人均月用水量(单位:![]() )的分组及各组的频数如下:
)的分组及各组的频数如下:
![]() ,4;
,4; ![]() ,8;
,8; ![]() ,15;
,15;
![]() ,22;
,22; ![]() ,25;
,25; ![]() ,14;
,14;
![]() ,6;
,6; ![]() ,4;
,4; ![]() ,2.
,2.
(1)列出样本的频率分布表;
(2)画出频率分布直方图,并根据直方图估计这组数据的平均数、中位数、众数;
(3)当地政府制定了人均月用水量为![]() 的标准,若超出标准加倍收费,当地政府说,
的标准,若超出标准加倍收费,当地政府说,![]() 以上的居民不超过这个标准,这个解释对吗?为什么?
以上的居民不超过这个标准,这个解释对吗?为什么?
参考答案:
【答案】(1)分布表见解析;(2)直方图见解析;平均数为2.02, 中位数为2.02,众数为2.25;(3)政府的解释是正确的,原因见解析.
【解析】
(1)根据已知数据计算频率,填入频率分布表即可;(2)根据每组数据和对应的频率可画出频率分布直方图,根据直方图估计平均数、中位数和众数的方法分别计算即可;(3)计算出月用水量超过![]() 的比例,由此可得不超过
的比例,由此可得不超过![]() 的比例为
的比例为![]() ,由此可知政府的解释是正确的.
,由此可知政府的解释是正确的.
(1)频率分布表如下:
分组 | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
|
(2)频率分布直方图如图:
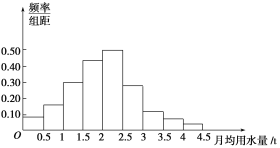
众数为:![]()
月用水量在![]() 的频率为:
的频率为:![]()
![]()
![]() 中位数为:
中位数为:![]()
平均数为:![]()
![]()
(3)人均月用水量在![]() 以上的居民所占的比例为
以上的居民所占的比例为![]()
即大约有![]() 的居民月用水量在
的居民月用水量在![]() 以上,
以上,![]() 的居民月用水量在
的居民月用水量在![]() 以下
以下
因此政府的解释是正确的
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地区有小学21所,中学14所,大学7所,现采取分层抽样的方法从这些学校中抽取6所学校对学生进行视力调查。
(I)求应从小学、中学、大学中分别抽取的学校数目。
(II)若从抽取的6所学校中随机抽取2所学校做进一步数据分析,
(1)列出所有可能的抽取结果;
(2)求抽取的2所学校均为小学的概率。
-
科目: 来源: 题型:
查看答案和解析>>【题目】从某企业生产的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得如下频率分布直方图:

(1)求这500件产品质量指标值的样本平均数 和样本方差s2(同一组中数据用该组区间的中点值作代表);
和样本方差s2(同一组中数据用该组区间的中点值作代表);
(2)由直方图可以认为,这种产品的质量指标值Z服从正态分布N(μ,σ2),其中μ近似为样本平均数 ,σ2近似为样本方差s2 .
,σ2近似为样本方差s2 .
(i)利用该正态分布,求P(187.8<Z<212.2);
(ii)某用户从该企业购买了100件这种产品,记X表示这100件产品中质量指标值位于区间(187.8,212.2)的产品件数,利用(i)的结果,求EX.
附: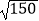 ≈12.2.
≈12.2.
若Z~N(μ,σ2)则P(μ﹣σ<Z<μ+σ)=0.6826,P(μ﹣2σ<Z<μ+2σ)=0.9544. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三棱柱ABC﹣A1B1C1中,侧面BB1C1C为菱形,AB⊥B1C.

(1)证明:AC=AB1;
(2)若AC⊥AB1 , ∠CBB1=60°,AB=BC,求二面角A﹣A1B1﹣C1的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
 为圆
为圆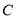 上任一点.
上任一点.(1)求
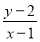 的最大值与最小值;
的最大值与最小值;(2)求
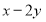 的最大值与最小值.
的最大值与最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知双曲线
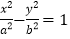 (b>a>0),O为坐标原点,离心率
(b>a>0),O为坐标原点,离心率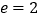 ,点
,点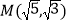 在双曲线上.
在双曲线上. (1)求双曲线的方程;
(2)若直线
 与双曲线交于P、Q两点,且
与双曲线交于P、Q两点,且 .求|OP|2+|OQ|2的最小值.
.求|OP|2+|OQ|2的最小值.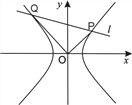
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)若
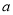 ,
, 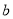 都是从0,1,2,3,4五个数中任取的一个数,求上述函数有零点的概率;
都是从0,1,2,3,4五个数中任取的一个数,求上述函数有零点的概率;(2)若
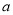 ,
,  都是从区间
都是从区间 上任取的一个数,求
上任取的一个数,求 成立的概率.
成立的概率.
相关试题

