【题目】已知双曲线![]() (b>a>0),O为坐标原点,离心率
(b>a>0),O为坐标原点,离心率![]() ,点
,点![]() 在双曲线上.
在双曲线上.
(1)求双曲线的方程;
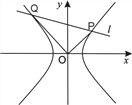
(2)若直线![]() 与双曲线交于P、Q两点,且
与双曲线交于P、Q两点,且![]() .求|OP|2+|OQ|2的最小值.
.求|OP|2+|OQ|2的最小值.
参考答案:
【答案】![]() 1
1![]()
![]() ;
;![]() 2
2![]() .
.
【解析】试题分析:
(Ⅰ) 由![]() ,可得
,可得![]() ,故双曲线方程为
,故双曲线方程为![]() ,代入点
,代入点![]() 的坐标可得
的坐标可得![]() ,由此可得双曲线方程. (Ⅱ)根据直线
,由此可得双曲线方程. (Ⅱ)根据直线![]() 的斜率存在与否分两种情况求解.当斜率存在时,可根据一元二次方程根与系数的关系及两点间的距离公式求解即可.当斜率不存在时直接计算可得结果.
的斜率存在与否分两种情况求解.当斜率存在时,可根据一元二次方程根与系数的关系及两点间的距离公式求解即可.当斜率不存在时直接计算可得结果.
试题解析:
(1)由![]() ,可得
,可得![]() ,
,
∴![]() ,
,
∴ 双曲线方程为![]() ,
,
∵ 点![]() 在双曲线上,
在双曲线上,
∴![]() ,
,
解得 ![]() ,
,
∴ 双曲线的方程为![]() .
.
(2)①当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为
的方程为![]() ,
,
由![]() 消去y整理得
消去y整理得![]() ,
,
∵直线![]() 与双曲线交于
与双曲线交于![]() 两点,
两点,
∴![]() .
.
设![]() ,
,![]() ,
,
则![]() ,
,
由![]() 得到:
得到:![]() ,
,
即![]() ,
,
∴![]() ,
,
化简得![]() .
.
∴![]() ,
,
当![]() 时上式取等号,且方程(*)有解.
时上式取等号,且方程(*)有解.
②当直线![]() 的斜率不存在时,设直线
的斜率不存在时,设直线![]() 的方程为
的方程为![]() ,则有
,则有![]() ,
,
由![]() 可得
可得![]() ,
,
可得![]() ,解得
,解得![]() .
.
∴![]() .
.
∴![]()
![]() .
.
综上可得![]() 的最小值是24.
的最小值是24.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三棱柱ABC﹣A1B1C1中,侧面BB1C1C为菱形,AB⊥B1C.

(1)证明:AC=AB1;
(2)若AC⊥AB1 , ∠CBB1=60°,AB=BC,求二面角A﹣A1B1﹣C1的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某地区100位居民的人均月用水量(单位:
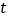 )的分组及各组的频数如下:
)的分组及各组的频数如下: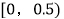 ,4;
,4; 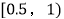 ,8;
,8; 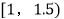 ,15;
,15; 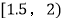 ,22;
,22; 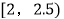 ,25;
,25; 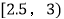 ,14;
,14;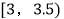 ,6;
,6; 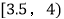 ,4;
,4;  ,2.
,2.(1)列出样本的频率分布表;
(2)画出频率分布直方图,并根据直方图估计这组数据的平均数、中位数、众数;
(3)当地政府制定了人均月用水量为
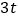 的标准,若超出标准加倍收费,当地政府说,
的标准,若超出标准加倍收费,当地政府说,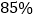 以上的居民不超过这个标准,这个解释对吗?为什么?
以上的居民不超过这个标准,这个解释对吗?为什么? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
 为圆
为圆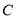 上任一点.
上任一点.(1)求
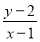 的最大值与最小值;
的最大值与最小值;(2)求
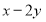 的最大值与最小值.
的最大值与最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)若
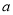 ,
, 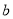 都是从0,1,2,3,4五个数中任取的一个数,求上述函数有零点的概率;
都是从0,1,2,3,4五个数中任取的一个数,求上述函数有零点的概率;(2)若
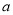 ,
,  都是从区间
都是从区间 上任取的一个数,求
上任取的一个数,求 成立的概率.
成立的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(0,﹣2),椭圆E:
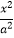 +
+ 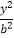 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为  ,F是椭圆的焦点,直线AF的斜率为
,F是椭圆的焦点,直线AF的斜率为 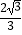 ,O为坐标原点.
,O为坐标原点.
(1)求E的方程;
(2)设过点A的直线l与E相交于P,Q两点,当△OPQ的面积最大时,求l的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=aexlnx+
 ,曲线y=f(x)在点(1,f(1))处得切线方程为y=e(x﹣1)+2.
,曲线y=f(x)在点(1,f(1))处得切线方程为y=e(x﹣1)+2.
(1)求a、b;
(2)证明:f(x)>1.
相关试题

