【题目】已知函数![]() .
.
(1)若![]() ,
, ![]() 都是从0,1,2,3,4五个数中任取的一个数,求上述函数有零点的概率;
都是从0,1,2,3,4五个数中任取的一个数,求上述函数有零点的概率;
(2)若![]() ,
, ![]() 都是从区间
都是从区间![]() 上任取的一个数,求
上任取的一个数,求![]() 成立的概率.
成立的概率.
参考答案:
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:
(1)基本事件总数为![]() 个.函数有零点的条件为
个.函数有零点的条件为![]() .
.![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,则函数
,则函数![]() 有零点的概率为
有零点的概率为![]() .
.
(2)由几何概型的计算公式可得事件“![]() ”的概率为
”的概率为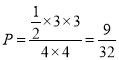 .
.
试题解析:
解:(1)![]() ,
, ![]() 都是从0,1,2,3,4五个数中任取的一个数,则基本事件总数为
都是从0,1,2,3,4五个数中任取的一个数,则基本事件总数为![]() 个.
个.
函数有零点的条件为![]() ,即
,即![]() .因为事件“
.因为事件“![]() ”包含
”包含![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
所以事件“![]() ”的概率为
”的概率为![]() ,即函数
,即函数![]() 有零点的概率为
有零点的概率为![]() .
.
(2)![]() ,
, ![]() 都是从区间
都是从区间![]() 上任取的一个数,
上任取的一个数, ![]() ,即
,即![]() ,此为几何模型,如图可知,事件“
,此为几何模型,如图可知,事件“![]() ”的概率为
”的概率为 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地区100位居民的人均月用水量(单位:
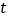 )的分组及各组的频数如下:
)的分组及各组的频数如下: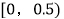 ,4;
,4; 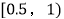 ,8;
,8; 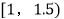 ,15;
,15; 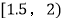 ,22;
,22; 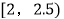 ,25;
,25; 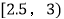 ,14;
,14;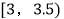 ,6;
,6; 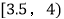 ,4;
,4;  ,2.
,2.(1)列出样本的频率分布表;
(2)画出频率分布直方图,并根据直方图估计这组数据的平均数、中位数、众数;
(3)当地政府制定了人均月用水量为
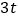 的标准,若超出标准加倍收费,当地政府说,
的标准,若超出标准加倍收费,当地政府说,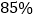 以上的居民不超过这个标准,这个解释对吗?为什么?
以上的居民不超过这个标准,这个解释对吗?为什么? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
 为圆
为圆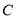 上任一点.
上任一点.(1)求
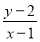 的最大值与最小值;
的最大值与最小值;(2)求
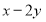 的最大值与最小值.
的最大值与最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知双曲线
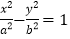 (b>a>0),O为坐标原点,离心率
(b>a>0),O为坐标原点,离心率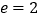 ,点
,点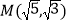 在双曲线上.
在双曲线上. (1)求双曲线的方程;
(2)若直线
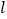 与双曲线交于P、Q两点,且
与双曲线交于P、Q两点,且 .求|OP|2+|OQ|2的最小值.
.求|OP|2+|OQ|2的最小值.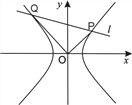
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(0,﹣2),椭圆E:
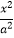 +
+ 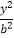 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为  ,F是椭圆的焦点,直线AF的斜率为
,F是椭圆的焦点,直线AF的斜率为 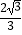 ,O为坐标原点.
,O为坐标原点.
(1)求E的方程;
(2)设过点A的直线l与E相交于P,Q两点,当△OPQ的面积最大时,求l的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=aexlnx+
 ,曲线y=f(x)在点(1,f(1))处得切线方程为y=e(x﹣1)+2.
,曲线y=f(x)在点(1,f(1))处得切线方程为y=e(x﹣1)+2.
(1)求a、b;
(2)证明:f(x)>1. -
科目: 来源: 题型:
查看答案和解析>>【题目】等比数列{an}的各项均为正数,且2a1+3a2=1,
 =9a2a6.
=9a2a6.(1)求数列{an}的通项公式;
(2)设bn=log3a1+log3a2+…+log3an,求数列
 的前n项和.
的前n项和.
相关试题

