【题目】从某企业生产的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得如下频率分布直方图:
(1)求这500件产品质量指标值的样本平均数 ![]() 和样本方差s2(同一组中数据用该组区间的中点值作代表);
和样本方差s2(同一组中数据用该组区间的中点值作代表);
(2)由直方图可以认为,这种产品的质量指标值Z服从正态分布N(μ,σ2),其中μ近似为样本平均数 ![]() ,σ2近似为样本方差s2 .
,σ2近似为样本方差s2 .
(i)利用该正态分布,求P(187.8<Z<212.2);
(ii)某用户从该企业购买了100件这种产品,记X表示这100件产品中质量指标值位于区间(187.8,212.2)的产品件数,利用(i)的结果,求EX.
附: ![]() ≈12.2.
≈12.2.
若Z~N(μ,σ2)则P(μ﹣σ<Z<μ+σ)=0.6826,P(μ﹣2σ<Z<μ+2σ)=0.9544.
参考答案:
【答案】
(1)
解:抽取产品的质量指标值的样本平均数 ![]() 和样本方差s2分别为:
和样本方差s2分别为:
![]() =170×0.02+180×0.09+190×0.22+200×0.33+210×0.24+220×0.08+230×0.02=200,
=170×0.02+180×0.09+190×0.22+200×0.33+210×0.24+220×0.08+230×0.02=200,
s2=(﹣30)2×0.02+(﹣20)2×0.09+(﹣10)2×0.22+0×0.33+102×0.24+202×0.08+302×0.02=150.
(2)
解:(i)由(1)知Z~N(200,150),从而P(187.8<Z<212.2)=P(200﹣12.2<Z<200+12.2)=0.6826;
(ii)由(i)知一件产品的质量指标值位于区间(187.8,212.2)的概率为0.6826,
依题意知X~B(100,0.6826),所以EX=100×0.6826=68.26
【解析】(1)运用离散型随机变量的期望和方差公式,即可求出;(2)(i)由(1)知Z~N(200,150),从而求出P(187.8<Z<212.2),注意运用所给数据;(ii)由(i)知X~B(100,0.6826),运用EX=np即可求得.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知某运动员每次投篮命中的概率低于
 ,现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果,经随机模拟产生了如下20组随机数:
,现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果,经随机模拟产生了如下20组随机数:907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
据此估计,该运动员三次投篮恰有两次命中的概率为( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点p(1,m)在抛物线
 上,F为焦点,且
上,F为焦点,且 .
.(1)求抛物线C的方程;
(2)过点T(4,0)的直线
 交抛物线C于A,B两点,O为坐标原点,求
交抛物线C于A,B两点,O为坐标原点,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某地区有小学21所,中学14所,大学7所,现采取分层抽样的方法从这些学校中抽取6所学校对学生进行视力调查。
(I)求应从小学、中学、大学中分别抽取的学校数目。
(II)若从抽取的6所学校中随机抽取2所学校做进一步数据分析,
(1)列出所有可能的抽取结果;
(2)求抽取的2所学校均为小学的概率。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三棱柱ABC﹣A1B1C1中,侧面BB1C1C为菱形,AB⊥B1C.

(1)证明:AC=AB1;
(2)若AC⊥AB1 , ∠CBB1=60°,AB=BC,求二面角A﹣A1B1﹣C1的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某地区100位居民的人均月用水量(单位:
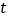 )的分组及各组的频数如下:
)的分组及各组的频数如下: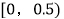 ,4;
,4; 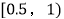 ,8;
,8; 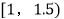 ,15;
,15; 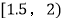 ,22;
,22; 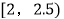 ,25;
,25; 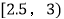 ,14;
,14;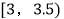 ,6;
,6; 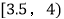 ,4;
,4;  ,2.
,2.(1)列出样本的频率分布表;
(2)画出频率分布直方图,并根据直方图估计这组数据的平均数、中位数、众数;
(3)当地政府制定了人均月用水量为
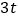 的标准,若超出标准加倍收费,当地政府说,
的标准,若超出标准加倍收费,当地政府说,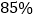 以上的居民不超过这个标准,这个解释对吗?为什么?
以上的居民不超过这个标准,这个解释对吗?为什么? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
 为圆
为圆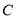 上任一点.
上任一点.(1)求
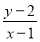 的最大值与最小值;
的最大值与最小值;(2)求
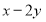 的最大值与最小值.
的最大值与最小值.
相关试题

