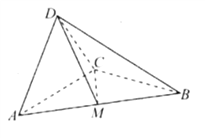
【题目】【2018江西抚州市高三八校联考】如图,在三棱锥![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() 为
为![]() 的中点.
的中点.
(I)求证: ![]() 平面
平面![]() ;
;
(II)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
参考答案:
【答案】(I)见解析;(II)![]()
【解析】试题分析:(1)利用勾股定理的逆定理得出![]() ,再用线面垂直的判定定理进行证明;(2)使用等体积法求出点
,再用线面垂直的判定定理进行证明;(2)使用等体积法求出点![]() 到平面
到平面![]() 的距离,进一步求出
的距离,进一步求出![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
试题解析:
∵![]() ,
, ![]() ,∴
,∴![]() .
.
又∵![]() ,∴
,∴![]() ,∴
,∴![]() .
.
∵平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
(2)取![]() 的中点
的中点![]() ,连接
,连接![]() ,
, ![]() ,在
,在![]() 中,
中, ![]() 且
且![]() .
.
又∵平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() .
.
∴![]() 平面
平面![]() .
.
在![]() 中,
中, ![]() 且
且![]() .
.
由(1)知![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
又∵![]() 平面
平面![]() ,∴
,∴![]() .∴
.∴![]()
在![]() 中,∵
中,∵![]() ,∴
,∴![]()
∴![]() 是等边三角形,∴
是等边三角形,∴![]()
设点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,则由
,则由![]() 得
得![]() ,
,
解得![]() .
.
设![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,则
,则![]() ,
,
∴直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】传承传统文化再掀热潮,央视科教频道以诗词知识竞赛为主的《中国诗词大会》火爆荧屏.将中学组和大学组的参赛选手按成绩分为优秀、良好、一般三个等级,随机从中抽取了100名选手进行调查,下面是根据调查结果绘制的选手等级人数的条形图.

(1)若将一般等级和良好等级合称为合格等级,根据已知条件完成下面的
 列联表,据此资料你是否有95%的把握认为选手成绩“优秀”与文化程度有关?
列联表,据此资料你是否有95%的把握认为选手成绩“优秀”与文化程度有关?优秀
合格
合计
大学组
中学组
合计
注:
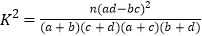 ,其中
,其中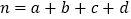 .
.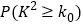
0.10
0.05
0.005
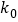
2.706
3.841
7.879
(2)若参赛选手共6万人,用频率估计概率,试估计其中优秀等级的选手人数.
(3)在优秀等级的选手中取6名,依次编号为1,2,3,4,5,6.在良好等级的选手中取6名,依次编号为1,2,3,4,5,6,在选出的6名优秀等级的选手中任取一名,记其编号为

,在选出的6名良好等级的选手中任取一名,记其编号为 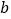 ,求使得方程组
,求使得方程组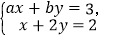 有唯一一组实数解
有唯一一组实数解 的概率.
的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
 :
:  的焦点
的焦点 与椭圆
与椭圆 :
:  的一个焦点重合,点
的一个焦点重合,点 在抛物线上,过焦点
在抛物线上,过焦点 的直线
的直线 交抛物线于
交抛物线于 、
、 两点.
两点. (Ⅰ)求抛物线
 的方程以及
的方程以及 的值;
的值;(Ⅱ)记抛物线的准线
 与
与 轴交于点
轴交于点 ,试问是否存在常数
,试问是否存在常数 ,使得
,使得 且
且 都成立?若存在,求出实数
都成立?若存在,求出实数 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
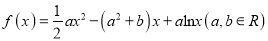
(Ⅰ)当
 时,求函数
时,求函数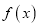 的单调区间;
的单调区间; (Ⅱ)当
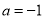 ,
,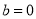 时,证明:
时,证明: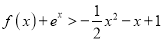 (其中
(其中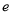 为自然对数的底数).
为自然对数的底数). -
科目: 来源: 题型:
查看答案和解析>>【题目】【2018四川南充高三第二次(3月)高考适应性考试】某校开展“翻转合作学习法”教学试验,经过一年的实践后,对“翻转班”和“对照班”的全部220名学生的数学学习情况进行测试,按照大于或等于120分为“成绩优秀”,120分以下为“成绩一般”统计,得到如下的
 列联表:
列联表:成绩优秀
成绩一般
合计
对照班
20
90
110
翻转班
40
70
110
合计
60
160
220
(I)根据上面的列联表判断,能否在犯错误的概率不超过0.001的前提下认为“成绩优秀与翻转合作学习法”有关;
(II)为了交流学习方法,从这次测试数学成绩优秀的学生中,用分层抽样方法抽出6名学生,再从这6名学生中抽3名出来交流学习方法,求至少抽到1名“对照班”学生交流的概率.
附表:
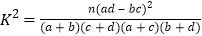
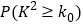
0.10
0.05
0.025
0.010
0.005
0.001
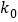
2.706
3.841
5.024
6.635
7.879
10.828
-
科目: 来源: 题型:
查看答案和解析>>【题目】【2018四川南充市高三第二次(3月)高考适应性考试】已知椭圆
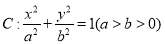 的离心率为
的离心率为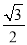 ,点
,点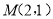 在椭圆
在椭圆 上.
上.(I)求椭圆
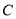 的方程;
的方程;(II)直线
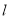 平行于
平行于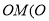 为坐标原点),且与椭圆
为坐标原点),且与椭圆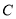 交于
交于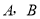 两个不同的点,若
两个不同的点,若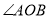 为钝角,求直线
为钝角,求直线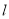 在
在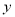 轴上的截距
轴上的截距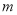 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系
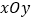 中,曲线
中,曲线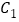 的参数方程为
的参数方程为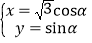 (其中
(其中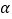 为参数),曲线
为参数),曲线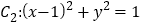 ,以坐标原点
,以坐标原点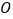 为极点,以
为极点,以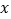 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.(1)求曲线
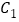 的普通方程和曲线
的普通方程和曲线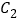 的极坐标方程;
的极坐标方程;(2)若射线
 与曲线
与曲线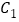 ,
,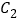 分别交于
分别交于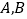 两点,求
两点,求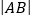 .
.
相关试题

