【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (其中
(其中![]() 为参数),曲线
为参数),曲线![]() ,以坐标原点
,以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的极坐标方程;
的极坐标方程;
(2)若射线![]() 与曲线
与曲线![]() ,
,![]() 分别交于
分别交于![]() 两点,求
两点,求![]() .
.
参考答案:
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]()
【解析】试题分析:(1)由sin2α+cos2α=1,能求出曲线C1的普通方程,由x=ρcosθ,y=ρsinθ,能求出曲线C2的极坐标方程;(2)依题意设A(![]() ),B(
),B(![]() ),将
),将![]() 代入曲线C1的极坐标方程,求出ρ1=3,将
代入曲线C1的极坐标方程,求出ρ1=3,将![]() (ρ>0)代入曲线C2的极坐标方程求出
(ρ>0)代入曲线C2的极坐标方程求出![]() ,由此能求出|AB|.
,由此能求出|AB|.
解析:
(Ⅰ)由![]() 得
得![]() .
.
所以曲线![]() 的普通方程为
的普通方程为![]() .
.
把![]() ,代入
,代入![]() ,得到
,得到![]() ,化简得到曲线
,化简得到曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅱ)依题意可设![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
将![]() 代入
代入![]() 的极坐标方程得
的极坐标方程得![]() ,解得
,解得![]() .
.
将![]() 代入
代入![]() 的极坐标方程得
的极坐标方程得![]() .
.
所以![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥
 中,底面
中,底面 是边长为
是边长为 的菱形,
的菱形,  .
.(1)求证:平面
 平面
平面 ;
;(2)若
 ,求锐角二面角
,求锐角二面角 的余弦值.
的余弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
 为圆
为圆 的圆心,
的圆心,  是圆上的动点,点
是圆上的动点,点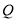 在圆的半径
在圆的半径 上,且有点
上,且有点 和
和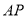 上的点
上的点 ,满足
,满足 ,
,  .
.(1)当点
 在圆上运动时,求点
在圆上运动时,求点 的轨迹方程;
的轨迹方程;(2)若斜率为
 的直线
的直线 与圆
与圆 相切,直线
相切,直线 与(1)中所求点
与(1)中所求点 的轨迹交于不同的两点
的轨迹交于不同的两点 ,
,  ,
,  是坐标原点,且
是坐标原点,且 时,求
时,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
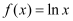 ,
,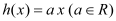 .
.(Ⅰ)函数
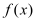 的图象与
的图象与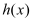 的图象无公共点,求实数
的图象无公共点,求实数 的取值范围;
的取值范围;(Ⅱ)是否存在实数
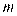 ,使得对任意的
,使得对任意的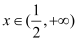 ,都有函数
,都有函数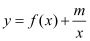 的图象在
的图象在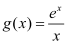 的图象的下方?若存在,请求出整数
的图象的下方?若存在,请求出整数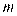 的最大值;若不存在,请说理由.
的最大值;若不存在,请说理由.(参考数据:
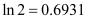 ,
,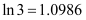 ,
,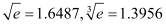 ).
). -
科目: 来源: 题型:
查看答案和解析>>【题目】祖暅原理也就是“等积原理”,它是由我国南北朝杰出的数学家祖冲之的儿子祖暅首先提出来的,祖暅原理的内容是:夹在两个平行平面间的两个几何体,被平行于这两个平行平面的平面所截,如果截得两个截面的面积总相等,那么这两个几何体的体积相等.已知,两个平行平面间有三个几何体,分别是三棱锥、四棱锥、圆锥(高度都为
 ),其中:三棱锥的底面是正三角形(边长为
),其中:三棱锥的底面是正三角形(边长为 ),四棱锥的底面是有一个角为
),四棱锥的底面是有一个角为 的菱形(边长为
的菱形(边长为 ),圆锥的体积为
),圆锥的体积为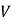 ,现用平行于这两个平行平面的平面去截三个几何体,如果截得的三个截面的面积相等,那么,下列关系式正确的是( )
,现用平行于这两个平行平面的平面去截三个几何体,如果截得的三个截面的面积相等,那么,下列关系式正确的是( )A.
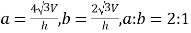 B.
B. 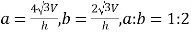
C.
 D.
D. 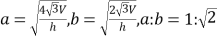
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱柱
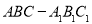 中,已知
中,已知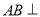 侧面
侧面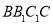 ,
,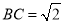 ,
,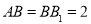 ,
,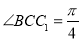 ,点
,点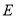 在棱
在棱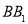 上.
上.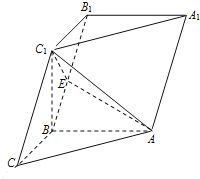
(Ⅰ)求证:
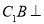 平面
平面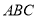 ;
;(Ⅱ)试确定点
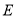 的位置,使得二面角
的位置,使得二面角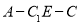 的余弦值为
的余弦值为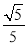 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】为评估设备
 生产某种零件的性能,从设备
生产某种零件的性能,从设备 生产零件的流水线上随机抽取100件零件作为样本,测量其直径后,整理得到下表:
生产零件的流水线上随机抽取100件零件作为样本,测量其直径后,整理得到下表:直径/

58
59
61
62
63
64
65
66
67
68
69
70
71
73
合计
件数
1
1
3
5
6
19
33
18
4
4
2
1
2
1
100
经计算,样本的平均值
 ,标准差
,标准差 ,以频率值作为概率的估计值.
,以频率值作为概率的估计值.(1)为评判一台设备的性能,从该设备加工的零件中任意抽取一件,记其直径为
 ,并根据以下不等式进行评判(
,并根据以下不等式进行评判( 表示相应事件的概率);
表示相应事件的概率);①
 ;
;②
 ;
;③

评判规则为:若同时满足上述三个不等式,则设备等级为甲;仅满足其中两个,则等级为乙;若仅满足其中一个,则等级为丙;若全部不满足,则等级为丁,试判断设备
 的性能等级.
的性能等级.(2)将直径小于等于
 或直径大于
或直径大于 的零件认为是次品.
的零件认为是次品.①从设备
 的生产流水线上随意抽取2件零件,计算其中次品个数
的生产流水线上随意抽取2件零件,计算其中次品个数 的数学期望
的数学期望 ;
;②从样本中随意抽取2件零件,计算其中次品个数
 的数学期望
的数学期望 .
.
相关试题

