【题目】已知函数![]()
(Ⅰ)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(Ⅱ)当![]() ,
,![]() 时,证明:
时,证明:![]() (其中
(其中![]() 为自然对数的底数).
为自然对数的底数).
参考答案:
【答案】(1)见解析;(2)见解析.
【解析】试题分析:(1)当![]() 时,
时, ![]() ,分类讨论:(1)
,分类讨论:(1)![]() ;(2)
;(2)![]() ,可得单调区间;(2)当
,可得单调区间;(2)当![]() 时,要 证
时,要 证
![]() 转化为证
转化为证![]() ,设
,设![]() ,判断其单调性,得
,判断其单调性,得![]() ,此题得证。
,此题得证。
(1)当![]() 时,
时, ![]()
![]()
![]()
讨论:1’当![]() 时,
时, ![]() ,
, ![]() ,
, ![]()
![]()
此时函数![]() 的单调递减区间为
的单调递减区间为![]() ,无单调递增区间
,无单调递增区间
2’当![]() 时,令
时,令![]()
![]() 或
或![]()
①当![]() ,即
,即![]() 时,此时
时,此时![]()
![]()
此时函数![]() 单调递增区间为
单调递增区间为![]() ,无单调递减区间
,无单调递减区间
②当![]() ,即
,即![]() 时,此时在
时,此时在![]() 和
和![]() 上函数
上函数![]() ,
,
在![]() 上函数
上函数![]() ,此时函数
,此时函数![]() 单调递增区间为
单调递增区间为![]() 和
和![]() ;
;
单调递减区间为![]()
③当![]() ,即
,即![]() 时,此时函数
时,此时函数![]() 单调递增区间为
单调递增区间为![]() 和
和![]() ;
;
单调递减区间为![]()
(2)证明:当![]() 时
时 ![]()
只需证明: ![]() 设
设![]()
![]()
问题转化为证明![]() ,
, ![]()
令![]() ,
, ![]() ,
,
![]() 为
为![]() 上的增函数,且
上的增函数,且![]() ,
, ![]()
![]() 存在唯一的
存在唯一的![]() ,使得
,使得![]() ,
, ![]()
![]() 在
在![]() 上递减,在
上递减,在![]() 上递增
上递增
![]()
![]()
![]()
![]() 不等式得证
不等式得证
-
科目: 来源: 题型:
查看答案和解析>>【题目】经国务院批复同意,重庆成功入围国家中心城市,某校学生社团针对“重庆的发展环境”对20名学生进行问卷调查打分(满分100分),得到如图所示茎叶图:
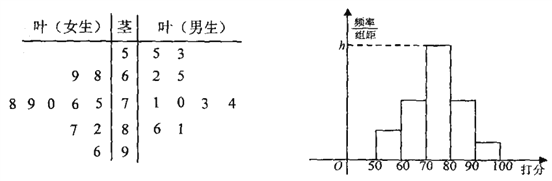
(Ⅰ)计算女生打分的平均分,并用茎叶图的数字特征评价男生、女生打分谁更分散;
(Ⅱ)如图按照打分区间
 、
、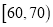 、
、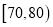 、
、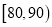 、
、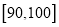 绘制的直方图中,求最高矩形的高
绘制的直方图中,求最高矩形的高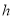 ;
;(Ⅲ)从打分在70分以下(不含70分)的同学中抽取3人,求有女生被抽中的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
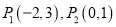 ,圆
,圆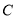 是以
是以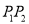 的中点为圆心,
的中点为圆心, 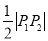 为半径的圆.
为半径的圆.(Ⅰ)若圆
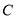 的切线在
的切线在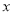 轴和
轴和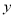 轴上截距相等,求切线方程;
轴上截距相等,求切线方程;(Ⅱ)若
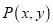 是圆
是圆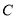 外一点,从
外一点,从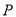 向圆
向圆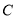 引切线
引切线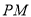 ,
,  为切点,
为切点, 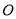 为坐标原点,且有
为坐标原点,且有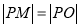 ,求使
,求使 最小的点
最小的点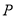 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】某教研机构随机抽取某校20个班级,调查各班关注汉字听写大赛的学生人数,根据所得数据的茎叶图,以组距为5将数据分组成
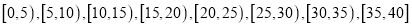 时,所作的频率分布直方图如图所示,则原始茎叶图可能是( )
时,所作的频率分布直方图如图所示,则原始茎叶图可能是( )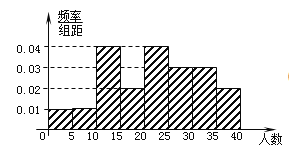
A.
 B.
B. 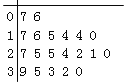
C.
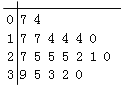 D.
D. 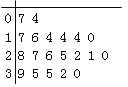
-
科目: 来源: 题型:
查看答案和解析>>【题目】某城市要建成宜商、宜居的国际化新城,该城市的东城区、西城区分别引进8个厂家,现对两个区域的16个厂家进行评估,综合得分情况如茎叶图所示.
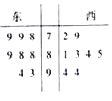
(1)根据茎叶图判断哪个区域厂家的平均分较高;
(2)规定85分以上(含85分)为优秀厂家,若从该两个区域各选一个优秀厂家,求得分差距不超过5分的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学高二年级开设五门大学先修课程,其中属于数学学科的有两门,分别是线性代数和微积分,其余三门分别为大学物理,商务英语以及文学写作,年级要求每名学生只能选修其中一科,该校高二年级600名学生各科选课人数统计如下表:

其中选修数学学科的人数所占频率为0.6,为了了解学生成绩与选课情况之间的关系,用分层抽样的方法从这600名学生中抽取10人进行分析.
(1)从选出的10名学生中随机抽取3人,求这3人中至少2人选修线性代数的概率;
(2)从选出的10名学生中随机抽取3人,记
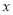 为选择线性代数人数与选择微积分人数差的绝对值,求随机变量
为选择线性代数人数与选择微积分人数差的绝对值,求随机变量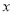 的分布列和数学期望.
的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知两条不重合的直线
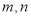 和两个不重合的平面
和两个不重合的平面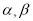 ,若
,若 ,则下列四个命题:①若
,则下列四个命题:①若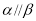 ,则
,则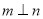 ;②若
;②若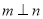 ,则
,则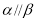 ; ③若
; ③若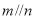 ,则
,则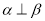 ;④若
;④若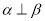 ,则
,则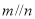 ,其中正确命题的个数是( )
,其中正确命题的个数是( )A. 0 B. 1 C. 2 D. 3
相关试题

