【题目】某高校从参加今年自主招生考试的学生中随机抽取容量为![]() 的学生成绩样本,得频率分布表如下:
的学生成绩样本,得频率分布表如下:
组号 | 分组 | 频率 | 频数 |
第一组 |
|
|
|
第二组 |
| ① |
|
第三组 |
|
| ② |
第四组 |
|
|
|
第五组 |
|
|
|
合计 |
|
| |
(1)写出表中①、②位置的数据;
(2)估计成绩不低于![]() 分的学生约占多少;
分的学生约占多少;
(3)为了选拔出更优秀的学生,高校决定在第三、四、五组中用分层抽样法抽取![]() 名学生进行第二轮考核,分别求第三、四、五各组参加考核的人数.
名学生进行第二轮考核,分别求第三、四、五各组参加考核的人数.
参考答案:
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 、
、![]() 、
、![]() .
.
【解析】
(1)利用频数之和为![]() 得出①中的数据,利用频率之和得出②中的数据;
得出①中的数据,利用频率之和得出②中的数据;
(2)将第三组、第四组、第五组频率相加得出答案;
(3)分别计算出第三、四、五组在样本中所占的比例,再分别乘以![]() 可得出第三、四、五各组参加考核的人数.
可得出第三、四、五各组参加考核的人数.
(1)由频数之和为![]() ,可知①中的数据为
,可知①中的数据为![]() ,
,
由频率之和为![]() ,可知②中的数据为
,可知②中的数据为![]() ;
;
(2)由题意可知,成绩不低于![]() 分的学生所占比为前三组频率之和,
分的学生所占比为前三组频率之和,
因此,成绩不低于![]() 分的学生所占比为
分的学生所占比为![]() ;
;
(3)由分层抽样的特点可知,第三组参加考核的人数为![]() ,
,
第四组参加考核的人数为![]() ,
,
第五组参加考核的人数为![]() ,
,
因此,第三、四、五各组参加考核的人数分别为![]() 、
、![]() 、
、![]() 。
。
-
科目: 来源: 题型:
查看答案和解析>>【题目】东莞市公交公司为了方便广大市民出行,科学规划公交车辆的投放,计划在某个人员密集流动地段增设一个起点站,为了研究车辆发车的间隔时间
 与乘客等候人数
与乘客等候人数 之间的关系,选取一天中的六个不同的时段进行抽样调查,经过统计得到如下数据:
之间的关系,选取一天中的六个不同的时段进行抽样调查,经过统计得到如下数据:间隔时间(
 分钟)
分钟)8
10
12
14
16
18
等候人数(
 人)
人)16
19
23
26
29
33
调查小组先从这6组数据中选取其中的4组数据求得线性回归方程,再用剩下的2组数据进行检验,检验方法如下:先用求得的线性回归方程计算间隔时间对应的等候人数
 ,再求
,再求 与实际等候人数
与实际等候人数 的差,若两组差值的绝对值均不超过1,则称所求的回归方程是“理想回归方程”.
的差,若两组差值的绝对值均不超过1,则称所求的回归方程是“理想回归方程”.参考公式:用最小二乘法求线性回归方程
 的系数公式:
的系数公式: ,
,(1)若选取的是前4组数据,求
 关于
关于 的线性回归方程
的线性回归方程 ;
;(2)判断(1)中的方程是否是“理想回归方程”:
(3)为了使等候的乘客不超过38人,试用(1)中方程估计间隔时间最多可以设置为多少分钟?
-
科目: 来源: 题型:
查看答案和解析>>【题目】从某小区抽取100户居民进行月用电量调查,发现其用电量都在50度至350度之间,频率分布直方图如图所示.

(1)根据直方图求x的值,并估计该小区100户居民的月均用电量(同一组中的数据用该组区间的中点值作代表);
(2)从该小区已抽取的100户居民中,随机抽取月用电量超过250度的3户,参加节约用电知识普及讲座,其中恰有ξ户月用电量超过300度,求ξ的分布列及期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆心在
 轴的正半轴上,且半径为2的圆
轴的正半轴上,且半径为2的圆 被直线
被直线 截得的弦长为
截得的弦长为 .
.(1)求圆
 的方程;
的方程;(2)设动直线
 与圆
与圆 交于
交于 两点,则在
两点,则在 轴正半轴上是否存在定点
轴正半轴上是否存在定点 ,使得直线
,使得直线 与直线
与直线 关于
关于 轴对称?若存在,请求出点
轴对称?若存在,请求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】袋子中装有除颜色外其他均相同的编号为a,b的两个黑球和编号为c,d,e的三个红球,从中任意摸出两个球.
(1)求恰好摸出1个黑球和1个红球的概率:
(2)求至少摸出1个黑球的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校研究性学习小组从汽车市场上随机抽取
 辆纯电动汽车调查其续驶里程(单次充电后能行驶的最大里程),被调查汽车的续驶里程全部介于
辆纯电动汽车调查其续驶里程(单次充电后能行驶的最大里程),被调查汽车的续驶里程全部介于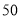 公里和
公里和 公里之间,将统计结果分成
公里之间,将统计结果分成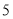 组:
组: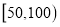 ,
, ,
, ,
, ,
, ,绘制成如图所示的频率分布直方图.
,绘制成如图所示的频率分布直方图.
(1)求直方图中
 的值;
的值;(2)求续驶里程在
 的车辆数;
的车辆数;(3)若从续驶里程在
 的车辆中随机抽取
的车辆中随机抽取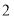 辆车,求其中恰有一辆车的续驶里程在
辆车,求其中恰有一辆车的续驶里程在 内的概率.
内的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直三棱柱ABC﹣A1B1C1中,AA1=AB=AC=2,D,E,F分别是B1A1 , CC1 , BC的中点,AE⊥A1B1 , D为棱A1B1上的点.

(1)证明:DF⊥AE;
(2)求平面DEF与平面ABC所成锐二面角的余弦值.
相关试题

