【题目】从某小区抽取100户居民进行月用电量调查,发现其用电量都在50度至350度之间,频率分布直方图如图所示. 
(1)根据直方图求x的值,并估计该小区100户居民的月均用电量(同一组中的数据用该组区间的中点值作代表);
(2)从该小区已抽取的100户居民中,随机抽取月用电量超过250度的3户,参加节约用电知识普及讲座,其中恰有ξ户月用电量超过300度,求ξ的分布列及期望.
参考答案:
【答案】
(1)解:由已知得50×(0.0012+0.0024×2+0.0036+x+0.0060)=1,
解得x=0.0044
设该小区100户居民的月均用电量为S,
则S=0.0024×50×75+0.0036×50×125+0.0060×50×175+0.0044×50×225+0.0024×50×275+0.0012×50×325=9+22.5+52.5+49.5+33+19.5=186
(2)该小区用电量在(250,300]的用户数为0.0024×50×100=12,
用电量在(300,350]的用户数为0.0012×50×100=6,
由已知得ξ的可能取值为0,1,2,3,
ξ=0时, ![]() ,
,
ξ=1时, ![]() ,
,
ξ=2时, ![]() ,
,
ξ=3时, ![]()
所以ξ的分布列是
ξ | 0 | 1 | 2 | 3 |
p |
|
|
|
|
E(ξ)=0×p(ξ=0)+1×p(ξ=1)+2×p(ξ=2)+3×p(ξ=3)=1.
【解析】(1)由已知得50×(0.0012+0.0024×2+0.0036+x+0.0060)=1,由此能求出x,由频率分布直方图能求出该小区100户居民的月均用电量.(2)由已知得ξ的可能取值为0,1,2,3,分别求出相应的概率,由此能求出ξ的分布列及期望.
【考点精析】掌握频率分布直方图和离散型随机变量及其分布列是解答本题的根本,需要知道频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息;在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列.
-
科目: 来源: 题型:
查看答案和解析>>【题目】东莞市摄影协会准备在2019年10月举办主题为“庆祖国70华诞——我们都是追梦人”摄影图片展.通过平常人的镜头记录国强民富的幸福生活,向祖国母亲的生日献礼,摄影协会收到了来自社会各界的大量作品,打算从众多照片中选取100张照片展出,其参赛者年龄集中在
 之间,根据统计结果,做出频率分布直方图如图:
之间,根据统计结果,做出频率分布直方图如图:
(1)求频率分布直方图中
 的值,并根据频率分布直方图,求这100位摄影者年龄的样本平均数
的值,并根据频率分布直方图,求这100位摄影者年龄的样本平均数 和中位数
和中位数 (同一组数据用该区间的中点值作代表);
(同一组数据用该区间的中点值作代表);(2)为了展示不同年龄作者眼中的祖国形象,摄影协会按照分层抽样的方法,计划从这100件照片中抽出20个最佳作品,并邀请相应作者参加“讲述照片背后的故事”座谈会.
①在答题卡上的统计表中填出每组相应抽取的人数:
年龄




人数
②若从年龄在
 的作者中选出2人把这些图片和故事整理成册,求这2人至少有一人的年龄在
的作者中选出2人把这些图片和故事整理成册,求这2人至少有一人的年龄在 的概率.
的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
 为菱形,
为菱形, ,
, 平面
平面 ,
, ,
, ,
, 为的中点.
为的中点.
(Ⅰ) 求证:

 平面
平面
(Ⅱ) 求证:

(Ⅲ)若
 为线段
为线段 上的点,当三棱锥
上的点,当三棱锥 的体积为
的体积为 时,求
时,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】东莞市公交公司为了方便广大市民出行,科学规划公交车辆的投放,计划在某个人员密集流动地段增设一个起点站,为了研究车辆发车的间隔时间
 与乘客等候人数
与乘客等候人数 之间的关系,选取一天中的六个不同的时段进行抽样调查,经过统计得到如下数据:
之间的关系,选取一天中的六个不同的时段进行抽样调查,经过统计得到如下数据:间隔时间(
 分钟)
分钟)8
10
12
14
16
18
等候人数(
 人)
人)16
19
23
26
29
33
调查小组先从这6组数据中选取其中的4组数据求得线性回归方程,再用剩下的2组数据进行检验,检验方法如下:先用求得的线性回归方程计算间隔时间对应的等候人数
 ,再求
,再求 与实际等候人数
与实际等候人数 的差,若两组差值的绝对值均不超过1,则称所求的回归方程是“理想回归方程”.
的差,若两组差值的绝对值均不超过1,则称所求的回归方程是“理想回归方程”.参考公式:用最小二乘法求线性回归方程
 的系数公式:
的系数公式: ,
,(1)若选取的是前4组数据,求
 关于
关于 的线性回归方程
的线性回归方程 ;
;(2)判断(1)中的方程是否是“理想回归方程”:
(3)为了使等候的乘客不超过38人,试用(1)中方程估计间隔时间最多可以设置为多少分钟?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆心在
 轴的正半轴上,且半径为2的圆
轴的正半轴上,且半径为2的圆 被直线
被直线 截得的弦长为
截得的弦长为 .
.(1)求圆
 的方程;
的方程;(2)设动直线
 与圆
与圆 交于
交于 两点,则在
两点,则在 轴正半轴上是否存在定点
轴正半轴上是否存在定点 ,使得直线
,使得直线 与直线
与直线 关于
关于 轴对称?若存在,请求出点
轴对称?若存在,请求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某高校从参加今年自主招生考试的学生中随机抽取容量为
 的学生成绩样本,得频率分布表如下:
的学生成绩样本,得频率分布表如下:组号
分组
频率
频数
第一组



第二组

①

第三组


②
第四组



第五组



合计


(1)写出表中①、②位置的数据;
(2)估计成绩不低于
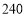 分的学生约占多少;
分的学生约占多少;(3)为了选拔出更优秀的学生,高校决定在第三、四、五组中用分层抽样法抽取
 名学生进行第二轮考核,分别求第三、四、五各组参加考核的人数.
名学生进行第二轮考核,分别求第三、四、五各组参加考核的人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】袋子中装有除颜色外其他均相同的编号为a,b的两个黑球和编号为c,d,e的三个红球,从中任意摸出两个球.
(1)求恰好摸出1个黑球和1个红球的概率:
(2)求至少摸出1个黑球的概率.
相关试题

