【题目】东莞市公交公司为了方便广大市民出行,科学规划公交车辆的投放,计划在某个人员密集流动地段增设一个起点站,为了研究车辆发车的间隔时间![]() 与乘客等候人数
与乘客等候人数![]() 之间的关系,选取一天中的六个不同的时段进行抽样调查,经过统计得到如下数据:
之间的关系,选取一天中的六个不同的时段进行抽样调查,经过统计得到如下数据:
间隔时间( | 8 | 10 | 12 | 14 | 16 | 18 |
等候人数( | 16 | 19 | 23 | 26 | 29 | 33 |
调查小组先从这6组数据中选取其中的4组数据求得线性回归方程,再用剩下的2组数据进行检验,检验方法如下:先用求得的线性回归方程计算间隔时间对应的等候人数![]() ,再求
,再求![]() 与实际等候人数
与实际等候人数![]() 的差,若两组差值的绝对值均不超过1,则称所求的回归方程是“理想回归方程”.
的差,若两组差值的绝对值均不超过1,则称所求的回归方程是“理想回归方程”.
参考公式:用最小二乘法求线性回归方程![]() 的系数公式:
的系数公式: ,
,
(1)若选取的是前4组数据,求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)判断(1)中的方程是否是“理想回归方程”:
(3)为了使等候的乘客不超过38人,试用(1)中方程估计间隔时间最多可以设置为多少分钟?
参考答案:
【答案】(1)![]() (2)是“理想回归方程”(3)估计间隔时间最多可以设置为21分钟
(2)是“理想回归方程”(3)估计间隔时间最多可以设置为21分钟
【解析】
(1)根据所给公式计算可得回归方程;
(2)由理想回归方程的定义验证;
(3)直接解不等式![]() 即可.
即可.
(1)![]() ,
,![]()
![]()
![]()
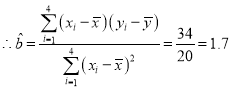
![]()
![]()
(2)![]()
当![]() 时,
时,![]()
当![]() 时,
时,![]()
![]() ,
,![]()
所以判断(1)中的方程![]() 是“理想回归方程”
是“理想回归方程”
(3)由![]() ,得
,得![]()
![]() 估计间隔时间最多可以设置为21分钟
估计间隔时间最多可以设置为21分钟
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班在一次个人投篮比赛中,记录了在规定时间内投进
 个球的人数分布情况:
个球的人数分布情况:进球数
 (个)
(个)0
1
2
3
4
5
投进
 个球的人数(人)
个球的人数(人)1
2
7
2
其中
 和
和 对应的数据不小心丢失了,已知进球3个或3个以上,人均投进4个球;进球5个或5个以下,人均投进2.5个球.
对应的数据不小心丢失了,已知进球3个或3个以上,人均投进4个球;进球5个或5个以下,人均投进2.5个球.(1)投进3个球和4个球的分别有多少人?
(2)从进球数为3,4,5的所有人中任取2人,求这2人进球数之和为8的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】东莞市摄影协会准备在2019年10月举办主题为“庆祖国70华诞——我们都是追梦人”摄影图片展.通过平常人的镜头记录国强民富的幸福生活,向祖国母亲的生日献礼,摄影协会收到了来自社会各界的大量作品,打算从众多照片中选取100张照片展出,其参赛者年龄集中在
 之间,根据统计结果,做出频率分布直方图如图:
之间,根据统计结果,做出频率分布直方图如图:
(1)求频率分布直方图中
 的值,并根据频率分布直方图,求这100位摄影者年龄的样本平均数
的值,并根据频率分布直方图,求这100位摄影者年龄的样本平均数 和中位数
和中位数 (同一组数据用该区间的中点值作代表);
(同一组数据用该区间的中点值作代表);(2)为了展示不同年龄作者眼中的祖国形象,摄影协会按照分层抽样的方法,计划从这100件照片中抽出20个最佳作品,并邀请相应作者参加“讲述照片背后的故事”座谈会.
①在答题卡上的统计表中填出每组相应抽取的人数:
年龄




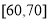
人数
②若从年龄在
 的作者中选出2人把这些图片和故事整理成册,求这2人至少有一人的年龄在
的作者中选出2人把这些图片和故事整理成册,求这2人至少有一人的年龄在 的概率.
的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
 为菱形,
为菱形, ,
, 平面
平面 ,
, ,
, ,
, 为的中点.
为的中点.
(Ⅰ) 求证:

 平面
平面
(Ⅱ) 求证:

(Ⅲ)若
 为线段
为线段 上的点,当三棱锥
上的点,当三棱锥 的体积为
的体积为 时,求
时,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】从某小区抽取100户居民进行月用电量调查,发现其用电量都在50度至350度之间,频率分布直方图如图所示.

(1)根据直方图求x的值,并估计该小区100户居民的月均用电量(同一组中的数据用该组区间的中点值作代表);
(2)从该小区已抽取的100户居民中,随机抽取月用电量超过250度的3户,参加节约用电知识普及讲座,其中恰有ξ户月用电量超过300度,求ξ的分布列及期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆心在
 轴的正半轴上,且半径为2的圆
轴的正半轴上,且半径为2的圆 被直线
被直线 截得的弦长为
截得的弦长为 .
.(1)求圆
 的方程;
的方程;(2)设动直线
 与圆
与圆 交于
交于 两点,则在
两点,则在 轴正半轴上是否存在定点
轴正半轴上是否存在定点 ,使得直线
,使得直线 与直线
与直线 关于
关于 轴对称?若存在,请求出点
轴对称?若存在,请求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某高校从参加今年自主招生考试的学生中随机抽取容量为
 的学生成绩样本,得频率分布表如下:
的学生成绩样本,得频率分布表如下:组号
分组
频率
频数
第一组



第二组

①

第三组


②
第四组



第五组



合计


(1)写出表中①、②位置的数据;
(2)估计成绩不低于
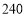 分的学生约占多少;
分的学生约占多少;(3)为了选拔出更优秀的学生,高校决定在第三、四、五组中用分层抽样法抽取
 名学生进行第二轮考核,分别求第三、四、五各组参加考核的人数.
名学生进行第二轮考核,分别求第三、四、五各组参加考核的人数.
相关试题

