【题目】如图,直三棱柱ABC﹣A1B1C1中,AA1=AB=AC=2,D,E,F分别是B1A1 , CC1 , BC的中点,AE⊥A1B1 , D为棱A1B1上的点. 
(1)证明:DF⊥AE;
(2)求平面DEF与平面ABC所成锐二面角的余弦值.
参考答案:
【答案】
(1)证明:∵AE⊥A1B1,A1B1∥AB,
∴AB⊥AE,又∵AB⊥AA1,AE∩AA1=A,
∴AB⊥面A1ACC1,又∵AC面A1ACC1,
∴AB⊥AC,
以A为原点,分别以AB,AC,AA1所在直线为x,y,z轴,
建立空间直角坐标系,
则A(0,0,0),E(0,2,1),F(1,1,0),A1(0,0,2),B1(2,0,2),
设D(x,y,z), ![]() =λ
=λ ![]() ,且λ∈[0,1],
,且λ∈[0,1],
即(x,y,z﹣2)=λ(2,0,0),∴D(2λ,0,2),
∴ ![]() =(1﹣2λ,1,﹣2),
=(1﹣2λ,1,﹣2), ![]() =(0,2,1),
=(0,2,1),
∵ ![]() =0+2﹣2=0,
=0+2﹣2=0,
∴DF⊥AE
(2)解: D(1,0,2),E(0,2,1),F(1,1,1),
![]() =(﹣1,2,﹣1),
=(﹣1,2,﹣1), ![]() =(0,1,﹣1),
=(0,1,﹣1),
设平面DEF的法向量 ![]() =(x,y,z),
=(x,y,z),
则  ,取y=1,得
,取y=1,得 ![]() =(1,1,1),
=(1,1,1),
平面ABC的法向量 ![]() =(0,0,1),
=(0,0,1),
cos< ![]() >=
>= ![]() =
= ![]() .
.
∴平面DEF与平面ABC所成锐二面角的余弦值为 ![]() .
.

【解析】(1)推导出AB⊥AE,AB⊥AA1 , 从而AB⊥面A1ACC1 , 由此能证明AB⊥AC,以A为原点,分别以AB,AC,AA1所在直线为x,y,z轴,建立空间直角坐标系,利用向量法能证明DF⊥AE.(2)求出平面DEF的法向量和平面ABC的法向量,利用向量法能求出平面DEF与平面ABC所成锐二面角的余弦值.
【考点精析】解答此题的关键在于理解空间中直线与直线之间的位置关系的相关知识,掌握相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某高校从参加今年自主招生考试的学生中随机抽取容量为
 的学生成绩样本,得频率分布表如下:
的学生成绩样本,得频率分布表如下:组号
分组
频率
频数
第一组



第二组

①

第三组


②
第四组



第五组



合计


(1)写出表中①、②位置的数据;
(2)估计成绩不低于
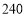 分的学生约占多少;
分的学生约占多少;(3)为了选拔出更优秀的学生,高校决定在第三、四、五组中用分层抽样法抽取
 名学生进行第二轮考核,分别求第三、四、五各组参加考核的人数.
名学生进行第二轮考核,分别求第三、四、五各组参加考核的人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】袋子中装有除颜色外其他均相同的编号为a,b的两个黑球和编号为c,d,e的三个红球,从中任意摸出两个球.
(1)求恰好摸出1个黑球和1个红球的概率:
(2)求至少摸出1个黑球的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校研究性学习小组从汽车市场上随机抽取
 辆纯电动汽车调查其续驶里程(单次充电后能行驶的最大里程),被调查汽车的续驶里程全部介于
辆纯电动汽车调查其续驶里程(单次充电后能行驶的最大里程),被调查汽车的续驶里程全部介于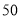 公里和
公里和 公里之间,将统计结果分成
公里之间,将统计结果分成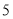 组:
组: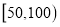 ,
, ,
, ,
, ,
, ,绘制成如图所示的频率分布直方图.
,绘制成如图所示的频率分布直方图.
(1)求直方图中
 的值;
的值;(2)求续驶里程在
 的车辆数;
的车辆数;(3)若从续驶里程在
 的车辆中随机抽取
的车辆中随机抽取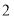 辆车,求其中恰有一辆车的续驶里程在
辆车,求其中恰有一辆车的续驶里程在 内的概率.
内的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】设椭圆C:
 =1(α>b>0)经过点(
=1(α>b>0)经过点(  ,
,  ),且原点、焦点,短轴的端点构成等腰直角三角形.
),且原点、焦点,短轴的端点构成等腰直角三角形.
(1)求椭圆E的方程;
(2)是否存在圆心在原点的圆,使得该圆的任意一条切线(切线斜率存在)与椭圆C恒有两个交点A,B.且 ?若存在,求出该圆的方程,若不存在说明理由.
?若存在,求出该圆的方程,若不存在说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=xlnx﹣ax2+(2a﹣1)x.
(1)若a= ,求函数f(x)的单调区间;
,求函数f(x)的单调区间;
(2)若x∈[1,+∞)时恒有f(x)≤a﹣1,求a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱柱
 中,侧面
中,侧面 是边长为2的正方形,点
是边长为2的正方形,点 是棱
是棱 的中点.
的中点.
(1)证明:
 平面
平面 .
.(2)若三棱锥
 的体积为4,求点
的体积为4,求点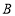 到平面
到平面 的距离.
的距离.
相关试题

