【题目】如图,在三棱柱ABC﹣A1B1C1中,底面为正三角形,侧棱垂直底面,AB=4,AA1=6,若E,F分别是棱BB1 , CC1上的点,且BE=B1E,C1F= ![]() CC1 , 则异面直线A1E与AF所成角的余弦值为( )
CC1 , 则异面直线A1E与AF所成角的余弦值为( ) 
A.![]()
B.![]()
C.![]()
D.![]()
参考答案:
【答案】D
【解析】解:以C为原点,CA为x轴,在平面ABC中过作AC的垂线为y轴,CC1为z轴,建立空间直角坐标系,
∵在三棱柱ABC﹣A1B1C1中,底面为正三角形,侧棱垂直底面,AB=4,AA1=6,
E,F分别是棱BB1 , CC1上的点,且BE=B1E,C1F= ![]() CC1 ,
CC1 ,
∴A1(4,0,6),E(2,2 ![]() ,3),F(0,0,4),A(4,0,0),
,3),F(0,0,4),A(4,0,0),![]() =(﹣2,2
=(﹣2,2 ![]() ,﹣3),
,﹣3), ![]() =(﹣4,0,4),
=(﹣4,0,4),
设异面直线A1E与AF所成角所成角为θ,
则cosθ= 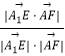 =
= ![]() =
= ![]() .
.
∴异面直线A1E与AF所成角的余弦值为 ![]() .
.
故选:D.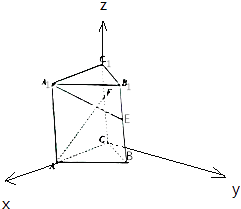
以C为原点,CA为x轴,在平面ABC中过作AC的垂线为y轴,CC1为z轴,建立空间直角坐标系,利用向量法能求出异面直线A1E与AF所成角的余弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
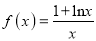 .
.(1)求函数
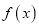 的极大值;
的极大值;(2)若函数
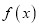 在区间
在区间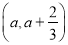
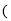 其中
其中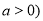 上存在极值,求实数
上存在极值,求实数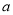 的取值范围;
的取值范围;(3)如果当
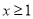 时,不等式
时,不等式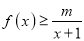 恒成立,求实数
恒成立,求实数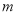 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义域为R的函数f(x)=
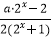 满足f(0)=0.
满足f(0)=0.
(1)求a,f(﹣2)的值,判断函数f(x)的奇偶性并说明理由;
(2)判断该函数在R上的单调性(不要求证明),解不等式f(x2+x)<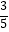 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知在△ABC中,角A,B,C的对边分别是a,b,c,向量m=(2b,1),n=(2a-c,cos C),且m∥n.(1)若b2=ac,试判断△ABC的形状;(2)求y=1-
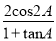 的值域.
的值域. -
科目: 来源: 题型:
查看答案和解析>>【题目】若不等式|2x﹣1|﹣|x+a|≥a对任意的实数x恒成立,则实数a的取值范围是( )
A.(﹣∞,﹣ ]
]
B.(﹣ ,﹣
,﹣  ]
]
C.(﹣ ,0)
,0)
D.(﹣∞,﹣ ]
] -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=a﹣
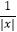 ,
,
(1)若x∈[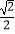 ,+∞),①判断函数g(x)=f(x)﹣2x的单调性并加以证明;②如果f(x)≤2x恒成立,求a的取值范围;
,+∞),①判断函数g(x)=f(x)﹣2x的单调性并加以证明;②如果f(x)≤2x恒成立,求a的取值范围;
(2)若总存在m,n使得当x∈[m,n]时,恰有f(x)∈[2m,2n],求a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数g(x)=ex , f(x)=
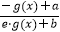 ,f(x)是定义在R上的奇函数.
,f(x)是定义在R上的奇函数.
(1)求a,b的值;
(2)若关于t的方程f(2t2﹣mt)+f(1﹣t2)=0有两个根α、β,且α>0,1<β<2,求实数m的取值范围.
相关试题

