搜索
【题目】已知函数
.
（1）求函数
的极大值；
（2）若函数
在区间
其中
上存在极值，求实数
的取值范围；
（3）如果当
时，不等式
恒成立，求实数
的取值范围.
参考答案：
【答案】（1）函数
在
处取得极大值
（2）
（3）
【解析】试题分析：（1）先求导数，再求导函数零点，列表分析导函数符号变化规律，进而确定函数极大值（2）由题意1必在区间
内，解不等式可得实数
的取值范围；（3）先分离变量将不等式恒成立问题转化为对应函数最值问题，再利用导数研究函数最值，即得实数
的取值范围.
试题解析：解:（1）函数
的定义域为
， 
，
当
时， 
， 
在
上单调递增
当
时， 
， 
在
上单调递减
函数
在
处取得极大值
（2）
函数
在区间
上存在极值
， 解得
当
时，不等式
，即为
记
，则
令
，则
在
上单调递增
， 从而
故
在
上单调递增
实数
的取值范围是
-
科目： 来源： 题型：
查看答案和解析>>【题目】等比数列{an}的各项均为正数，且2a1＋3a2＝1，
＝9a2a6.(1)求数列{an}的通项公式；
(2)设bn＝log3a1＋log3a2＋…＋log3an，求数列
的前n项和． -
科目： 来源： 题型：
查看答案和解析>>【题目】选修4－4：坐标系与参数方程
已知曲线
的参数方程为
（
为参数），在同一平面直角坐标系中，将曲线
上的点按坐标变换
得到曲线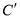
．（1）求曲线
的普通方程；（2）若点
在曲线
上，点
，当点
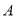在曲线
上运动时，求
中点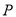
的轨迹方程． -
科目： 来源： 题型：
查看答案和解析>>【题目】空间四边形ABCD中，AB=CD且异面直线AB与CD所成的角为30°，E，F为BC和AD的中点，则异面直线EF和AB所成的角为（ ）
A.15°
B.30°
C.45°或75°
D.15°或75° -
科目： 来源： 题型：
查看答案和解析>>【题目】已知定义域为R的函数f（x）=
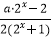满足f（0）=0．
（1）求a，f（﹣2）的值，判断函数f（x）的奇偶性并说明理由；
（2）判断该函数在R上的单调性（不要求证明），解不等式f（x2+x）＜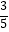
． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知在△ABC中，角A，B，C的对边分别是a，b，c，向量m＝(2b，1)，n＝(2a－c，cos C)，且m∥n.(1)若b2＝ac，试判断△ABC的形状；(2)求y＝1－
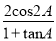的值域． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在三棱柱ABC﹣A1B1C1中，底面为正三角形，侧棱垂直底面，AB=4，AA1=6，若E，F分别是棱BB1 ， CC1上的点，且BE=B1E，C1F=
CC1 ， 则异面直线A1E与AF所成角的余弦值为（ ） 
A.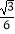
B.
C.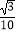
D.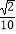
相关试题
