【题目】已知定义域为R的函数f(x)= ![]() 满足f(0)=0.
满足f(0)=0.
(1)求a,f(﹣2)的值,判断函数f(x)的奇偶性并说明理由;
(2)判断该函数在R上的单调性(不要求证明),解不等式f(x2+x)< ![]() .
.
参考答案:
【答案】
(1)解:∵f(x)= ![]() 且f(0)=0,
且f(0)=0,
∴ ![]() ,解得a=2.
,解得a=2.
∴ ![]() ,则
,则 ![]() .
.
∵ 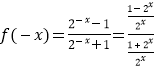 =
= ![]() =﹣f(x),
=﹣f(x),
∴f(x)为定义域内的奇函数;
(2)解: ![]() .
.
f(x)为实数集上的增函数,
由f(x2+x)< ![]() ,得f(x2+x)<
,得f(x2+x)< ![]() =f(2),
=f(2),
∴x2+x<2,解得﹣2<x<1.
∴不等式f(x2+x)< ![]() 的解集为(﹣2,1)
的解集为(﹣2,1)
【解析】(1)直接由f(0)=0求得a的值,得到函数解析式,求得f(﹣2)的值,再由函数奇偶性的判定方法判断奇偶性;(2)由函数解析式 ![]() 可判断函数为实数集上的增函数,把
可判断函数为实数集上的增函数,把 ![]() 用f(2)代替后利用单调性转化为二次不等式求解.
用f(2)代替后利用单调性转化为二次不等式求解.
【考点精析】关于本题考查的函数的奇偶性和指、对数不等式的解法,需要了解偶函数的图象关于y轴对称;奇函数的图象关于原点对称;指数不等式的解法规律:根据指数函数的性质转化;对数不等式的解法规律:根据对数函数的性质转化才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
已知曲线
 的参数方程为
的参数方程为 (
( 为参数),在同一平面直角坐标系中,将曲线
为参数),在同一平面直角坐标系中,将曲线 上的点按坐标变换
上的点按坐标变换 得到曲线
得到曲线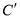 .(1)求曲线
.(1)求曲线 的普通方程;(2)若点
的普通方程;(2)若点 在曲线
在曲线 上,点
上,点
 ,当点
,当点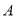 在曲线
在曲线 上运动时,求
上运动时,求 中点
中点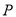 的轨迹方程.
的轨迹方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】空间四边形ABCD中,AB=CD且异面直线AB与CD所成的角为30°,E,F为BC和AD的中点,则异面直线EF和AB所成的角为( )
A.15°
B.30°
C.45°或75°
D.15°或75° -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
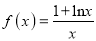 .
.(1)求函数
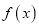 的极大值;
的极大值;(2)若函数
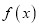 在区间
在区间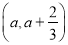
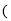 其中
其中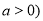 上存在极值,求实数
上存在极值,求实数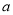 的取值范围;
的取值范围;(3)如果当
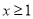 时,不等式
时,不等式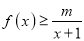 恒成立,求实数
恒成立,求实数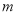 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知在△ABC中,角A,B,C的对边分别是a,b,c,向量m=(2b,1),n=(2a-c,cos C),且m∥n.(1)若b2=ac,试判断△ABC的形状;(2)求y=1-
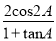 的值域.
的值域. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱柱ABC﹣A1B1C1中,底面为正三角形,侧棱垂直底面,AB=4,AA1=6,若E,F分别是棱BB1 , CC1上的点,且BE=B1E,C1F=
 CC1 , 则异面直线A1E与AF所成角的余弦值为( )
CC1 , 则异面直线A1E与AF所成角的余弦值为( ) 
A.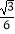
B.
C.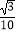
D.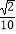
-
科目: 来源: 题型:
查看答案和解析>>【题目】若不等式|2x﹣1|﹣|x+a|≥a对任意的实数x恒成立,则实数a的取值范围是( )
A.(﹣∞,﹣ ]
]
B.(﹣ ,﹣
,﹣  ]
]
C.(﹣ ,0)
,0)
D.(﹣∞,﹣ ]
]
相关试题

