【题目】已知![]() 且
且![]() ,直线:
,直线: ![]() ,圆
,圆![]() :
:![]()
![]() .
.
(Ⅰ)若![]() ,请判断直线与圆
,请判断直线与圆![]() 的位置关系;
的位置关系;
(Ⅱ)求直线倾斜角![]() 的取值范围;
的取值范围;
(Ⅲ)直线能否将圆![]() 分割成弧长的比值为
分割成弧长的比值为![]() 的两段圆弧?为什么?
的两段圆弧?为什么?
参考答案:
【答案】(1) 直线与圆![]() 相交;(2)
相交;(2) ![]() ;(3)直线不能将圆
;(3)直线不能将圆![]() 分割成弧长的比值为
分割成弧长的比值为![]() 的两段弧.
的两段弧.
【解析】试题分析:(Ⅰ)若![]() ,求出圆心C(4,﹣2)到直线l的距离,与半径的关系,即可判断直线l与圆C的位置关系;
,求出圆心C(4,﹣2)到直线l的距离,与半径的关系,即可判断直线l与圆C的位置关系;
(Ⅱ)直线![]() ,可得:
,可得: ![]() ,利用均值不等式,即可得到直线倾斜角
,利用均值不等式,即可得到直线倾斜角![]() 的取值范围;
的取值范围;
(Ⅲ)判断![]() .若直线l能将圆C分割成弧长的比值为
.若直线l能将圆C分割成弧长的比值为![]() 的两段圆弧,则圆心C到直线l的距离
的两段圆弧,则圆心C到直线l的距离![]() ,即可得出结论.
,即可得出结论.
试题解析:
(Ⅰ)圆![]() 的圆心为
的圆心为![]() ,半径
,半径![]() .
.
若![]() ,直线:
,直线: ![]() ,即
,即![]() ,
,
则圆心![]() 到直线的距离
到直线的距离 ,
,
所以直线与圆![]() 相交.
相交.
(Ⅱ)直线的方程可化为![]() ,
,
直线的斜率![]() ,所以
,所以![]() ,当且仅当
,当且仅当![]() 时等号成立.
时等号成立.
所以斜率的取值范围是![]() .
.
所以![]() 的范围为
的范围为![]()
(Ⅲ)能.由(Ⅰ)知直线恒过点![]() ,
,
设直线的方程为![]() ,其中
,其中![]() .
.
圆心![]() 到直线的距离
到直线的距离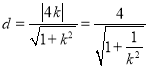 .
.
由![]() 得
得![]() ,又
,又![]() 即
即![]() .
.
若直线能将圆![]() 分割成弧长的比值为
分割成弧长的比值为![]() 的两段圆弧,则圆心
的两段圆弧,则圆心![]() 到直线的距离
到直线的距离![]() ,
,
因为![]() ,所以直线不能将圆
,所以直线不能将圆![]() 分割成弧长的比值为
分割成弧长的比值为![]() 的两段弧.
的两段弧.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为大力提倡“厉行节约,反对浪费”,某市通过随机询问100名性别不同的居民是否能做到“光盘”行动,得到如下的列联表:( )
做不到“光盘”
能做到“光盘”
男
45
10
女
30
15
附:
P(K2
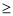 k)
k)0.10
0.05
0.025
k
2.706
3.841
5.024
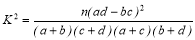
参照附表,得到的正确结论是
A.在犯错误的概率不超过l%的前提下,认为“该市居民能否做到‘光盘’与性别有关”
B.在犯错误的概率不超过l%的前提下,认为“该市居民能否做到‘光盘’与性别无关”
C.有90%以上的把握认为“该市居民能否做到‘光盘’与性别有关”
D.有90%以上的把握认为“该市居民能否做到‘光盘’与性别无关”
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD中,
 =(3,2),
=(3,2), 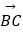 =(x,y),
=(x,y), 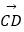 =(﹣2,﹣3)
=(﹣2,﹣3)
(1)若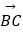 ∥
∥ 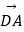 ,试求x与y满足的关系式;
,试求x与y满足的关系式;
(2)满足(1)同时又有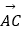 ⊥
⊥ 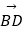 ,求x,y的值及四边形ABCD的面积.
,求x,y的值及四边形ABCD的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
, 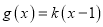 .
.(Ⅰ)证明:
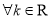 ,直线
,直线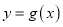 都不是曲线
都不是曲线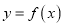 的切线;
的切线;(Ⅱ)若
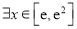 ,使
,使 成立,求实数
成立,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列五个命题:①“若
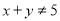 ,则
,则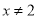 或
或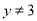 ”是假命题;②从正方体的面对角线中任取两条作为一对,其中所成角为
”是假命题;②从正方体的面对角线中任取两条作为一对,其中所成角为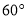 的有48对;③“
的有48对;③“ 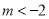 ”是方程
”是方程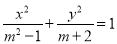 表示焦点在
表示焦点在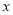 轴上的双曲线的充分不必要条件;④点
轴上的双曲线的充分不必要条件;④点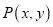 是曲线
是曲线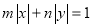 (
(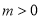 ,
, 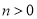 )上的动点,且满足
)上的动点,且满足 ,则
,则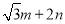 的取值范围是
的取值范围是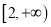 ;⑤若随机变量
;⑤若随机变量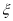 服从正态分布
服从正态分布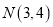 ,且
,且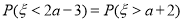 ,则
,则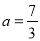 .其中正确命题的序号是__________(请把正确命题的序号填在横线上).
.其中正确命题的序号是__________(请把正确命题的序号填在横线上). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)=2
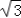 sinxcosx+2cos2x﹣1.
sinxcosx+2cos2x﹣1.(1)求f(x)的最大值,以及该函数取最大值时x的取值集合;
(2)在△ABC中,a、b、c分别是角A、B、C所对的边长,且
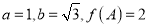 ,求角C.
,求角C. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在棱柱
 的面底是菱形,且
的面底是菱形,且 面ABCD,
面ABCD,  为棱
为棱 的中点,M为线段
的中点,M为线段 的中点.
的中点.(1)求证:平面
 平面
平面 ;
;(2)求三棱锥
 的体积.
的体积.
相关试题

