【题目】已知点![]() ,圆
,圆![]() 是以
是以![]() 的中点为圆心,
的中点为圆心, ![]() 为半径的圆.
为半径的圆.
(Ⅰ)若圆![]() 的切线在
的切线在![]() 轴和
轴和![]() 轴上截距相等,求切线方程;
轴上截距相等,求切线方程;
(Ⅱ)若![]() 是圆
是圆![]() 外一点,从
外一点,从![]() 向圆
向圆![]() 引切线
引切线![]() ,
, ![]() 为切点,
为切点, ![]() 为坐标原点,且有
为坐标原点,且有![]() ,求使
,求使![]() 最小的点
最小的点![]() 的坐标.
的坐标.
参考答案:
【答案】(Ⅰ)![]() ,
, ![]() 或
或![]() (Ⅱ)
(Ⅱ)![]()
【解析】试题分析:(Ⅰ)求出圆心与半径,可得圆C的方程,再分类讨论,设出切线方程,利用直线是切线建立方程,即可得出结论;(Ⅱ)先确定P的轨迹方程,再利用要使|PM|最小,只要|PO|最小即可
试题解析:(Ⅰ)设圆心坐标为![]() ,半径为
,半径为![]() ,依题意得
,依题意得
![]()
∴圆![]() 的方程为
的方程为![]()
(1)若截距均为0,即圆![]() 的切线过原点,则可设该切线为
的切线过原点,则可设该切线为![]() 即
即![]() ,
,
则有![]() ,解得
,解得![]() ,
,
此时切线方程为![]() 或
或![]() .
.
(2)若截距不为0,可设切线为![]() 即
即![]() ,
,
依题意![]() ,解得
,解得![]() 或3
或3
此时切线方程为![]() 或
或![]() .
.
综上:所求切线方程为![]() ,
, ![]() 或
或![]()
(Ⅱ)∵![]() ,∴
,∴![]()
即![]() 整理得
整理得![]()
而![]() ,
,
![]() 时
时![]() 取得最小值
取得最小值
此时点![]() 的坐标为
的坐标为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2017年五一假期期间,高速公路车辆较多。某调査公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调 査,将他们在某段高速公路的车速
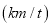 分成六段:
分成六段: 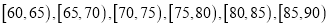 后得到如图的频率分布直方图.
后得到如图的频率分布直方图.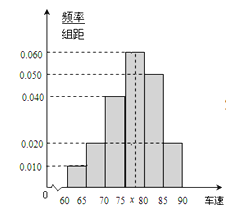
(Ⅰ)求这40辆小型车辆车速的众数和中位数以及平均数的估计值.
(Ⅱ)若从车速在
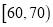 的车辆中任抽取2辆,求车速在
的车辆中任抽取2辆,求车速在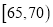 的车辆恰有一辆的概率.
的车辆恰有一辆的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知城
 和城
和城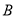 相距
相距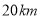 ,现计划以
,现计划以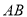 为直径的半圆上选择一点
为直径的半圆上选择一点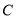 (不与点
(不与点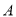 ,
, 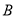 重合)建造垃圾处理厂.垃圾处理厂对城市的影响度与所选地点到城市的距离有关,对城
重合)建造垃圾处理厂.垃圾处理厂对城市的影响度与所选地点到城市的距离有关,对城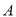 和城
和城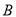 的总影响度为对城
的总影响度为对城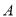 与城
与城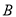 的影响度之和.记点到
的影响度之和.记点到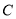 城
城 的距离为
的距离为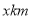 ,建在
,建在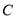 处的垃圾处理厂对城
处的垃圾处理厂对城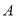 和城
和城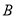 的总影响度为
的总影响度为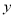 .统计调查表明:垃圾处理厂对城
.统计调查表明:垃圾处理厂对城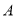 的影响度与所选地点到城
的影响度与所选地点到城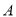 的距离的平方成反比例关系,比例系数为4;对城
的距离的平方成反比例关系,比例系数为4;对城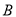 的影响度与所选地点到城
的影响度与所选地点到城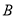 的距离的平方成反比例关系,比例系数为
的距离的平方成反比例关系,比例系数为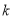 .当垃圾处理厂建在
.当垃圾处理厂建在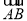 的中点时,对城
的中点时,对城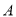 和城
和城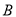 的总影响度为0.065.
的总影响度为0.065.(1)将
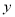 表示成
表示成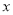 的函数.
的函数.(2)讨论(1)中函数的单调性,并判断在
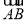 上是否存在一点,使建在此处的垃圾处理厂对城
上是否存在一点,使建在此处的垃圾处理厂对城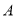 和城
和城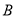 的总影响度最小?若存在,求出该点到城
的总影响度最小?若存在,求出该点到城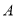 的距离;若不存在,请说明理由.
的距离;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】经国务院批复同意,重庆成功入围国家中心城市,某校学生社团针对“重庆的发展环境”对20名学生进行问卷调查打分(满分100分),得到如图所示茎叶图:
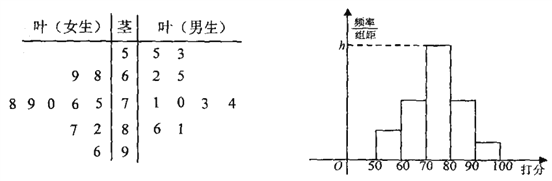
(Ⅰ)计算女生打分的平均分,并用茎叶图的数字特征评价男生、女生打分谁更分散;
(Ⅱ)如图按照打分区间
 、
、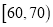 、
、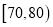 、
、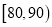 、
、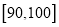 绘制的直方图中,求最高矩形的高
绘制的直方图中,求最高矩形的高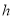 ;
;(Ⅲ)从打分在70分以下(不含70分)的同学中抽取3人,求有女生被抽中的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某教研机构随机抽取某校20个班级,调查各班关注汉字听写大赛的学生人数,根据所得数据的茎叶图,以组距为5将数据分组成
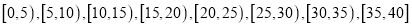 时,所作的频率分布直方图如图所示,则原始茎叶图可能是( )
时,所作的频率分布直方图如图所示,则原始茎叶图可能是( )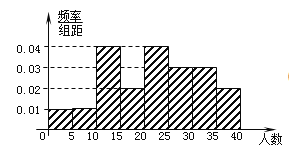
A.
 B.
B. 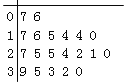
C.
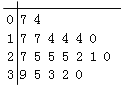 D.
D. 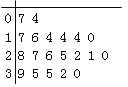
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
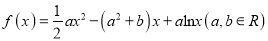
(Ⅰ)当
 时,求函数
时,求函数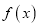 的单调区间;
的单调区间; (Ⅱ)当
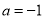 ,
,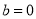 时,证明:
时,证明: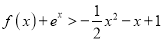 (其中
(其中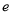 为自然对数的底数).
为自然对数的底数). -
科目: 来源: 题型:
查看答案和解析>>【题目】某城市要建成宜商、宜居的国际化新城,该城市的东城区、西城区分别引进8个厂家,现对两个区域的16个厂家进行评估,综合得分情况如茎叶图所示.
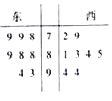
(1)根据茎叶图判断哪个区域厂家的平均分较高;
(2)规定85分以上(含85分)为优秀厂家,若从该两个区域各选一个优秀厂家,求得分差距不超过5分的概率.
相关试题

