【题目】已知城![]() 和城
和城![]() 相距
相距![]() ,现计划以
,现计划以![]() 为直径的半圆上选择一点
为直径的半圆上选择一点![]() (不与点
(不与点![]() ,
, ![]() 重合)建造垃圾处理厂.垃圾处理厂对城市的影响度与所选地点到城市的距离有关,对城
重合)建造垃圾处理厂.垃圾处理厂对城市的影响度与所选地点到城市的距离有关,对城![]() 和城
和城![]() 的总影响度为对城
的总影响度为对城![]() 与城
与城![]() 的影响度之和.记点到
的影响度之和.记点到![]() 城
城![]() 的距离为
的距离为![]() ,建在
,建在![]() 处的垃圾处理厂对城
处的垃圾处理厂对城![]() 和城
和城![]() 的总影响度为
的总影响度为![]() .统计调查表明:垃圾处理厂对城
.统计调查表明:垃圾处理厂对城![]() 的影响度与所选地点到城
的影响度与所选地点到城![]() 的距离的平方成反比例关系,比例系数为4;对城
的距离的平方成反比例关系,比例系数为4;对城![]() 的影响度与所选地点到城
的影响度与所选地点到城![]() 的距离的平方成反比例关系,比例系数为
的距离的平方成反比例关系,比例系数为![]() .当垃圾处理厂建在
.当垃圾处理厂建在![]() 的中点时,对城
的中点时,对城![]() 和城
和城![]() 的总影响度为0.065.
的总影响度为0.065.
(1)将![]() 表示成
表示成![]() 的函数.
的函数.
(2)讨论(1)中函数的单调性,并判断在![]() 上是否存在一点,使建在此处的垃圾处理厂对城
上是否存在一点,使建在此处的垃圾处理厂对城![]() 和城
和城![]() 的总影响度最小?若存在,求出该点到城
的总影响度最小?若存在,求出该点到城![]() 的距离;若不存在,请说明理由.
的距离;若不存在,请说明理由.
参考答案:
【答案】(1)![]() .
.
(2)点![]() 到城
到城![]() 的距离为
的距离为![]() 时,函数
时,函数![]() 有最小值.
有最小值.
【解析】(1)由点![]() 是在以
是在以![]() 为直径的半圆上,则易知
为直径的半圆上,则易知![]() ,由勾股定理可得,
,由勾股定理可得, ![]() ,再根据题意建立函数模型,求出系数
,再根据题意建立函数模型,求出系数![]() ,从而问题可得解;(2)由(1)可得,利用函数导数来研究该的单调性,并求出其最小值,从而问题可得解.
,从而问题可得解;(2)由(1)可得,利用函数导数来研究该的单调性,并求出其最小值,从而问题可得解.
试题解析:(1)由题意知![]() ,
, ![]() ,
, ![]() ,
,
则![]() ,
,
所以![]()
![]() .
.
因为当![]() 时,
时, ![]() ,
,
代入表达式解得![]() ,
,
所以![]()
![]() .
.
(2)因为![]() ,
,
所以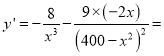
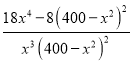 .
.
令![]() ,得
,得![]() ,
,
所以![]() ,即
,即![]() .
.
当![]() 时,
时, ![]() ,所以函数
,所以函数![]() 为减函数;
为减函数;
当![]() 时,
时, ![]() ,所以函数
,所以函数![]() 为增函数.
为增函数.
所以当![]() ,即点
,即点![]() 到城
到城![]() 的距离为
的距离为![]()
![]() 时,函数
时,函数![]()
![]() 有最小值.
有最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某土特产销售总公司为了解其经营状况,调查了其下属各分公司月销售额和利润,得到数据如下表:
分公司名称
雅雨
雅鱼
雅女
雅竹
雅茶
月销售额
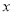 (万元)
(万元)3
5
6
7
9
月利润额
 (万元)
(万元)2
3
3
4
5
在统计中发现月销售额
 和月利润额
和月利润额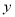 具有线性相关关系.
具有线性相关关系.(1)根据如下的参考公式与参考数据,求月利润额
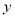 与月销售额
与月销售额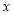 之间的线性回归方程;
之间的线性回归方程;(2)若该总公司还有一个分公司“雅果”月销售额为10万元,试估计它的月利润额是多少?
(参考公式:
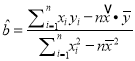 ,
, 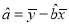 ,其中:
,其中: 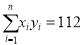 ,
, 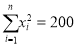 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】【选做题】本题包括A、B、C、D四小题,请选定其中两小题,并在相应的答题区域内作答.若多做,则按作答的前两小题评分.解答时应写出文字说明、证明过程或演算步骤.
A.[选修4-1:几何证明选讲]
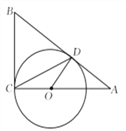
如图,
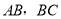 分别与圆
分别与圆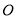 相切于点
相切于点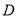 ,
, 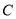 ,
, 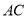 经过圆心
经过圆心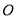 ,且
,且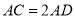 ,求证:
,求证: 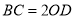 .
.
B.[选修4-2:矩阵与变换]
在平面直角坐标系中,已知点
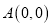 ,
, 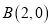 ,
, 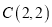 ,
, 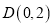 ,先将正方形
,先将正方形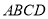 绕原点
绕原点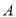 逆时针旋转
逆时针旋转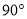 ,再将所得图形的纵坐标压缩为原来的一半、横坐标不变,求连续两次变换所对应的矩阵
,再将所得图形的纵坐标压缩为原来的一半、横坐标不变,求连续两次变换所对应的矩阵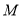 .
.C.[选修4-4:坐标系与参数方程]
在平面直角坐标系
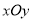 中,已知曲线
中,已知曲线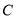 的参数方程为
的参数方程为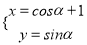 (
(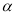 为参数).现以
为参数).现以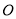 为极点,
为极点, 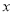 轴的正半轴为极轴,建立极坐标系,求曲线
轴的正半轴为极轴,建立极坐标系,求曲线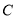 的极坐标方程.
的极坐标方程.D.[选修4-5:不等式选讲]
已知
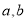 为互不相等的正实数,求证:
为互不相等的正实数,求证: 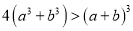 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】2017年五一假期期间,高速公路车辆较多。某调査公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调 査,将他们在某段高速公路的车速
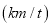 分成六段:
分成六段: 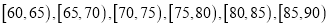 后得到如图的频率分布直方图.
后得到如图的频率分布直方图.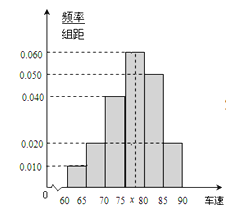
(Ⅰ)求这40辆小型车辆车速的众数和中位数以及平均数的估计值.
(Ⅱ)若从车速在
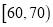 的车辆中任抽取2辆,求车速在
的车辆中任抽取2辆,求车速在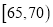 的车辆恰有一辆的概率.
的车辆恰有一辆的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】经国务院批复同意,重庆成功入围国家中心城市,某校学生社团针对“重庆的发展环境”对20名学生进行问卷调查打分(满分100分),得到如图所示茎叶图:
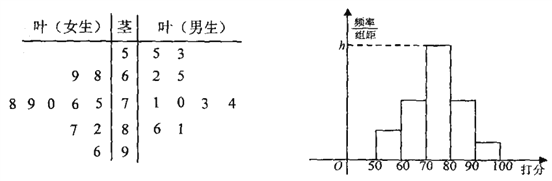
(Ⅰ)计算女生打分的平均分,并用茎叶图的数字特征评价男生、女生打分谁更分散;
(Ⅱ)如图按照打分区间
 、
、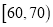 、
、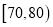 、
、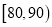 、
、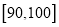 绘制的直方图中,求最高矩形的高
绘制的直方图中,求最高矩形的高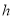 ;
;(Ⅲ)从打分在70分以下(不含70分)的同学中抽取3人,求有女生被抽中的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
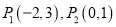 ,圆
,圆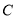 是以
是以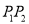 的中点为圆心,
的中点为圆心, 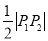 为半径的圆.
为半径的圆.(Ⅰ)若圆
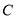 的切线在
的切线在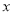 轴和
轴和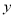 轴上截距相等,求切线方程;
轴上截距相等,求切线方程;(Ⅱ)若
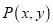 是圆
是圆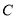 外一点,从
外一点,从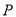 向圆
向圆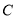 引切线
引切线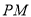 ,
,  为切点,
为切点, 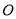 为坐标原点,且有
为坐标原点,且有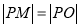 ,求使
,求使 最小的点
最小的点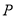 的坐标.
的坐标. -
科目: 来源: 题型:
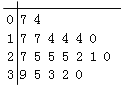
查看答案和解析>>【题目】某教研机构随机抽取某校20个班级,调查各班关注汉字听写大赛的学生人数,根据所得数据的茎叶图,以组距为5将数据分组成
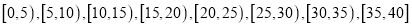 时,所作的频率分布直方图如图所示,则原始茎叶图可能是( )
时,所作的频率分布直方图如图所示,则原始茎叶图可能是( )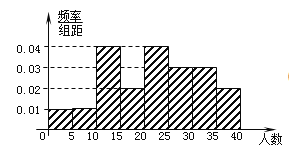
A.
 B.
B. 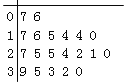
C.
 D.
D. 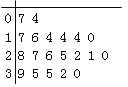
相关试题

