【题目】为了更好地服务民众,某共享单车公司通过![]() 向共享单车用户随机派送每张面额为0元,1元,2元的三种骑行券.用户每次使用
向共享单车用户随机派送每张面额为0元,1元,2元的三种骑行券.用户每次使用![]() 扫码用车后,都可获得一张骑行券.用户骑行一次获得1元奖券、获得2元奖券的概率分别是0.5、0.2,且各次获取骑行券的结果相互独立.
扫码用车后,都可获得一张骑行券.用户骑行一次获得1元奖券、获得2元奖券的概率分别是0.5、0.2,且各次获取骑行券的结果相互独立.
(I)求用户骑行一次获得0元奖券的概率;
(II)若某用户一天使用了两次该公司的共享单车,记该用户当天获得的骑行券面额之和为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
参考答案:
【答案】(I)![]() ;(II)
;(II)![]() (元).
(元).
【解析】分析:(1)利用对立事件概率公式可得用户骑行一次获得0元奖券的概率;
(2)由(1)知,一次骑行用户获得0元的概率为![]() .X的所有可能取值分别为0,1,2,3,4.分别求出相应的概率,由此能求出X的分布列和数学期望
.X的所有可能取值分别为0,1,2,3,4.分别求出相应的概率,由此能求出X的分布列和数学期望
详解:(I)由题可知骑行一次用户获得0元奖券的概率为: ![]()
(II)由(I)知一次骑行用户获得0元的概率为![]() .
.
![]() 的所有可能取值分别为0,1,2,3,4.
的所有可能取值分别为0,1,2,3,4.
∵![]() ,
, ![]()
![]() ,
,
![]()
![]() ,
, ![]()
![]() ,
,
![]() ,
,
∴![]() 的分布列为:
的分布列为:

![]() 的数学期望为
的数学期望为![]()
![]() (元).
(元).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知某超市为顾客提供四种结账方式:现金、支付宝、微信、银联卡.若顾客甲没有银联卡,顾客乙只带了现金,顾客丙、丁用哪种方式结账都可以,这四名顾客购物后,恰好用了其中的三种结账方式,那么他们结账方式的可能情况有( )种
A. 19B. 7C. 26D. 12
-
科目: 来源: 题型:
查看答案和解析>>【题目】设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为
 =0.85x-85.71,则下列结论中不正确的是
=0.85x-85.71,则下列结论中不正确的是A. y与x具有正的线性相关关系
B. 回归直线过样本点的中心(
 ,
, )
)C. 若该大学某女生身高增加1cm,则其体重约增加0.85kg
D. 若该大学某女生身高为170cm,则可断定其体重比为58.79kg
-
科目: 来源: 题型:
查看答案和解析>>【题目】由数字1,2,3,4,5,6组成没有重复数字的三位数,偶数共有______个,其中个位数字比十位数字大的偶数共有______个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对某种书籍每册的成本费
 (元)与印刷册数
(元)与印刷册数 (千册)的数据作了初步处理,得到下面的散点图及一些统计量的值.
(千册)的数据作了初步处理,得到下面的散点图及一些统计量的值.






4.83
4.22
0.3775
60.17
0.60
-39.38
4.8

其中
 ,
, .
.为了预测印刷
 千册时每册的成本费,建立了两个回归模型:
千册时每册的成本费,建立了两个回归模型: ,
, .
.(1)根据散点图,你认为选择哪个模型预测更可靠?(只选出模型即可)
(2)根据所给数据和(1)中的模型选择,求
 关于
关于 的回归方程,并预测印刷
的回归方程,并预测印刷 千册时每册的成本费.
千册时每册的成本费.附:对于一组数据
 ,
, ,…,
,…, ,其回归方程
,其回归方程 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为: ,
,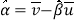 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】“回文数”是指从左到右与从右到左读都一样的正整数,如22,121,3553等.显然2位“回文数”共9个:11,22,33,…,99.现从9个不同2位“回文数”中任取1个乘以4,其结果记为X;从9个不同2位“回文数”中任取2个相加,其结果记为Y.
(1)求X为“回文数”的概率;
(2)设随机变量
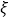 表示X,Y两数中“回文数”的个数,求
表示X,Y两数中“回文数”的个数,求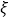 的概率分布和数学期望
的概率分布和数学期望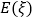 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】设集合
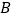 是集合
是集合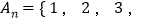 …,
…, 的子集.记
的子集.记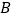 中所有元素的和为
中所有元素的和为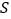 (规定:
(规定: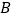 为空集时,
为空集时,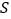 =0).若
=0).若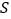 为3的整数倍,则称
为3的整数倍,则称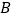 为
为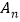 的“和谐子集”.
的“和谐子集”.求:(1)集合
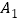 的“和谐子集”的个数;
的“和谐子集”的个数;(2)集合
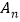 的“和谐子集”的个数.
的“和谐子集”的个数.
相关试题

