搜索
【题目】已知抛物线
，焦点为
，准线为
，线段
的中点为
.点
是
上在
轴上方的一点，且点到的距离等于它到原点
的距离.
（1）求点的坐标；
（2）过点
作一条斜率为正数的直线
与抛物线从左向右依次交于
两点，求证：
.
参考答案：
【答案】（1）
；（2）详见解析.
【解析】
（1）由点
到
的距离等于它到原点
的距离，得
，又
为线段
的中点，所以
，设点的坐标为
，代入抛物线的方程，解得
，即可得到点坐标.
（2）设直线
的方程为
，代入抛物线的方程，根据根与系数的关系，求得
，
，进而得到
，进而得到直线
和
的倾斜角互补，即可作出证明.
（1）根据抛物线的定义，点到的距离等于
，
因为点到的距离等于它到原点的距离，所以，
从而
为等腰三角形，
又为线段的中点，所以，
设点的坐标为，代入
，解得，
故点的坐标为.
（2）设直线的方程为，代入，并整理得
，
由直线与抛物线
交于
、
两点，得
，
结合
，解得
，
由韦达定理，得，，
，
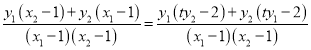
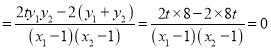所以直线和的倾斜角互补，从而
，
结合
轴，得
，故
.
-
科目： 来源： 题型：
查看答案和解析>>【题目】某商场销售某种商品的经验表明，该商品每日的销售量
（单位：千克）与销售价格
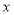（单位：元/千克）满足
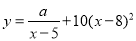，其中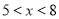
，
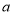为常数.已知销售价格为7元/千克时，每日可售出该商品11千克.（1）求
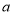的值；（2）若该商品成本为5元/千克，试确定销售价格
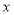值，使商场每日销售该商品所获利润最大. -
科目： 来源： 题型：
查看答案和解析>>【题目】某县畜牧技术员张三和李四9年来一直对该县山羊养殖业的规模进行跟踪调查，张三提供了该县某山羊养殖场年养殖数量y(单位：万只)与相成年份x(序号)的数据表和散点图(如图所示)，根据散点图，发现y与x有较强的线性相关关系，李四提供了该县山羊养殖场的个数z(单位：个)关于x的回归方程
.
(1)根据表中的数据和所给统计量，求y关于x的线性回归方程(参考统计量：
)；(2)试估计：①该县第一年养殖山羊多少万只?
②到第几年，该县山羊养殖的数量与第一年相比缩小了?
附：对于一组数据
，其回归直线
的斜率和截距的最小二乘估计分别为
． -
科目： 来源： 题型：
查看答案和解析>>【题目】近年来，双十一购物狂欢节（简称“双11”）活动已成为中国电子商务行业年度盛事，某网络商家为制定2018年“双11”活动营销策略，调查了2017年“双11”活动期间每位网购客户用于网购时间
（单位：小时），发现近似服从正态分布
．（1）求
的估计值；（2）该商家随机抽取参与2017年“双11”活动的10000名网购客户，这10000名客户在2017年“双11”活动期间，用于网购时间
属于区间
的客户数为
．该商家计划在2018年“双11”活动前对这名客户发送广告，所发广告的费用为每位客户0.05元． （i）求该商家所发广告总费用的平均估计值；
（ii）求使
取最大值时的整数
的值．附：若随机变量
服从正态分布
，则
， 
，
． -
科目： 来源： 题型：
查看答案和解析>>【题目】某代卖店代售的某种快餐，深受广大消费者喜爱，该种快餐每份进价为8元，并以每份12元的价格销售．如果当天19:00之前卖不完，剩余的该种快餐每份以5元的价格作特价处理，且全部售完．
（1）若这个代卖店每天定制15份该种快餐，求该种类型快餐当天的利润y（单位：元）关于当天需求量x（单位：份，
）的函数解析式；（2）该代卖点记录了一个月30天的每天19:00之前的销售数量该种快餐日需求量，统计数据如下：
日需求量
12
13
14
15
16
17
天数
4
5
6
8
4
3
以30天记录的日需求量的频率作为日需求量发生的概率，假设这个代卖店在这一个月内每天都定制15份该种快餐．
（i）求该种快餐当天的利润不少于52元的概率．
（ii）求这一个月该种快餐的日利润的平均数（精确到0.1）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在四面体
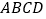中，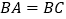
，
．
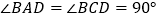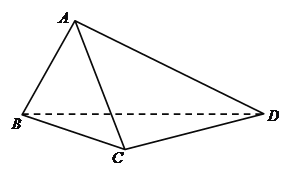
（1）证明：
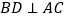；（2）若
，
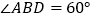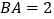，四面体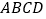的体积为2，证明：平面
平面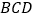
． -
科目： 来源： 题型：
查看答案和解析>>【题目】设函数
．（1）若
，讨论
的单调性；（2）若
在
上有两个零点，求
的取值范围．
相关试题
