【题目】庆华租赁公司拥有汽车100辆,当每辆车的月租金为3000元时,可全部租出,当每辆车的月租金每增加50元时,未租出的车将会增加一辆,租出的车每辆每月需维护费150元,未租出的车每辆每月需要维护费50元.
(1)当每辆车的月租金定为3600元时,能租出多少辆车?
(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?
参考答案:
【答案】(1)![]() ;(2)月租金定为
;(2)月租金定为![]() 元时,租赁公司的月收益最大,最大月收益是
元时,租赁公司的月收益最大,最大月收益是![]() 元.
元.
【解析】试题分析:(Ⅰ)当每辆车的月租金为x元时,租出的车辆![]() (辆),把x=3600代入计算;
(辆),把x=3600代入计算;
(Ⅱ)设每辆车的月租金为x元,租赁公司的月收益函数y,建立函数解析式,求出最大值即可
试题解析:(1)当每辆车月租金为3600时,未租出的车辆为![]() ,所以这时租出的车为100-12=88辆
,所以这时租出的车为100-12=88辆
(2)设每辆车的月租金定为![]() 元,则公司月收益为
元,则公司月收益为
![]() ∴当
∴当![]() 时,
时, ![]() 最大,最大值为
最大,最大值为![]() 元,所以当每辆车的月租金定为
元,所以当每辆车的月租金定为![]() 元时,租赁公司的月收益最大,最大月收益是
元时,租赁公司的月收益最大,最大月收益是![]() 元.
元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆心在x轴上的圆C与x轴交于两点A(1,0),B(5,0),此圆的标准方程为( )
A.(x-3)2+y2=4
B.(x+3)2+(y-1)2=4
C.(x-1)2+(y-1)2=4
D.(x+1)2+(y+1)2=4 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知平面α和直线l,则α内至少有一条直线与l( )
A. 异面 B. 相交 C. 平行 D. 垂直
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点P(a,a+1)在圆x2+y2=25内部,那么a的取值范围是( )
A.-4<a<3
B.-5<a<4
C.-5<a<5
D.-6<a<4 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知四棱锥
 的底面为直角梯形,
的底面为直角梯形, ,
, 底面
底面 ,且
,且 ,
, 是
是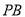 的中点.
的中点.
(1)证明:面
 面
面 ;
;(2)求直线
 与
与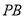 所成角的余弦值;
所成角的余弦值;(3)求二面角
 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】两平行线分别经过点A(5,0),B(0,12),它们之间的距离d满足的条件是( )
A.0<d≤5
B.0<d≤13
C.0<d<12
D.5≤d≤12 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)求函数
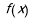 的极值;
的极值;(2)设函数
 ,若对
,若对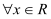 ,
, 恒不小于
恒不小于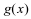 ,求
,求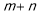 的最大值.
的最大值.
相关试题

