【题目】已知函数f(x)=m﹣|x﹣2|,m∈R,且f(x+2)≥0的解集为[﹣1,1].
(1)求m的值;
(2)若a,b,c∈R,且 ![]() =m,求证:a+2b+3c≥9.
=m,求证:a+2b+3c≥9.
参考答案:
【答案】
(1)解:函数f(x)=m﹣|x﹣2|,m∈R,故 f(x+2)=m﹣|x|,由题意可得m﹣|x|≥0的解集为[﹣1,1],
即|x|≤m 的解集为[﹣1,1],故m=1.
(2)证明:由a,b,c∈R,且 ![]() =1,
=1,
∴a+2b+3c=(a+2b+3c)( ![]() )
)
=1+ ![]() +1+
+1+ ![]() +1
+1
=3+ ![]() +
+ ![]() ≥3+6=9,当且仅当
≥3+6=9,当且仅当 ![]() =1时,等号成立.
=1时,等号成立.
所以a+2b+3c≥9
【解析】(1)由条件可得 f(x+2)=m﹣|x|,故有m﹣|x|≥0的解集为[﹣1,1],即|x|≤m 的解集为[﹣1,1],故m=1.(2)根据a+2b+3c=(a+2b+3c)( ![]() )=1+
)=1+ ![]() +1+
+1+ ![]() +1,利用基本不等式证明它大于或等于9.
+1,利用基本不等式证明它大于或等于9.
【考点精析】利用不等式的证明对题目进行判断即可得到答案,需要熟知不等式证明的几种常用方法:常用方法有:比较法(作差,作商法)、综合法、分析法;其它方法有:换元法、反证法、放缩法、构造法,函数单调性法,数学归纳法等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如今,中国的“双十一”已经从一个节日变成了全民狂欢的“电商购物日”.某淘宝电商分析近8年“双十一”期间的宣传费用
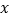 (单位:万元)和利润
(单位:万元)和利润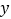 (单位:十万元)之间的关系,得到下列数据:
(单位:十万元)之间的关系,得到下列数据: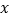
2
3
4
5
6
8
9
11
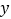
1
2
3
3
4
5
6
8
请回答:
(Ⅰ)请用相关系数
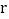 说明
说明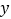 与
与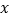 之间是否存在线性相关关系(当
之间是否存在线性相关关系(当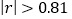 时,说明
时,说明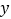 与
与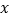 之间具有线性相关关系);
之间具有线性相关关系);(Ⅱ)根据1的判断结果,建立
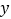 与
与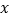 之间的回归方程,并预测当
之间的回归方程,并预测当 时,对应的利润
时,对应的利润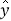 为多少(
为多少(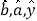 精确到
精确到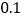 ).
).附参考公式:回归方程中
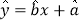 中
中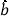 和
和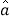 最小二乘估计分别为
最小二乘估计分别为 ,
,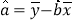 ,
,相关系数
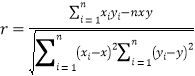 .
.参考数据:
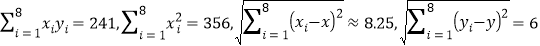 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
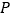 在抛物线
在抛物线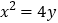 上,则当点
上,则当点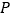 到点
到点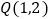 的距离与点
的距离与点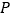 到抛物线焦点距离之和取得最小值时,点
到抛物线焦点距离之和取得最小值时,点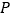 的坐标为( )
的坐标为( )A.
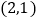 B.
B. 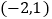 C.
C. 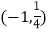 D.
D. 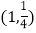
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴,建立极坐标系,曲线C1的参数方程为
 (θ为参数),曲线 C2的极坐标方程为ρcosθ﹣
(θ为参数),曲线 C2的极坐标方程为ρcosθ﹣  ρsinθ﹣4=0.
ρsinθ﹣4=0.
(1)求曲线C1的普通方程和曲线 C2的直角坐标方程;
(2)设P为曲线C1上一点,Q为曲线 C2上一点,求|PQ|的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.命题“x∈R,ex>0”的否定是“x∈R,ex>0”
B.命题“已知x,y∈R,若x+y≠3,则x≠2或y≠1”是真命题
C.“x2+2x≥ax在x∈[1,2]上恒成立”“(x2+2x)min≥(ax)max在x∈[1,2]上恒成立”
D.命题“若a=﹣1,则函数f(x)=ax2+2x﹣1只有一个零点”的逆命题为真命题 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=f(x)的定义在实数集R上的奇函数,且当x∈(﹣∞,0)时,xf′(x)<f(﹣x)(其中f′(x)是f(x)的导函数),若a=
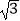 f(
f( 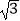 ),b=(lg3)f(lg3),c=(log2
),b=(lg3)f(lg3),c=(log2  )f(log2
)f(log2  ),则( )
),则( )
A.c>a>b
B.c>b>a
C.a>b>c
D.a>c>b -
科目: 来源: 题型:
查看答案和解析>>【题目】设点P是曲线y=x3﹣
 x+
x+  上的任意一点,点P处的切线倾斜角为α,则α的取值范围为 .
上的任意一点,点P处的切线倾斜角为α,则α的取值范围为 .
相关试题

