搜索
【题目】已知点
在抛物线
上，则当点到点
的距离与点到抛物线焦点距离之和取得最小值时，点的坐标为（ ）
A. 
B. 
C. 
D. 
参考答案：
【答案】D
【解析】
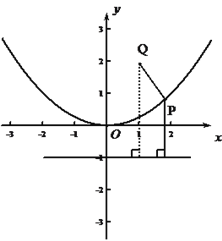
因为点
到抛物线焦点距离等于点到抛物线的准线
的距离，所以到点
的距离与点到抛物线焦点距离之和取得最小等价于到点的距离与点到抛物线准线距离之和取得最小，如图，由几何性质可得，从向准线作垂线，其与抛物线交点就是所求点，将
代入
，可得
，点到点的距离与点到抛物线焦点距离之和取得最小值时，点的坐标为
，故选D.
【方法点晴】本题主要考查抛物线的标准方程和抛物线的简单性质及利用抛物线的定义求最值，属于难题.与抛物线的定义有关的最值问题常常实现由点到点的距离与点到直线的距离的转化：(1)将抛物线上的点到准线的距化为该点到焦点的距离，构造出“两点之间线段最短”，使问题得解；(2)将拋物线上的点到焦点的距离转化为到准线的距离，利用“点与直线上所有点的连线中垂线段最短”原理解决.本题是将
到焦点的距离转化为到准线的距离，再根据几何意义解题的.
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知椭圆C：
(a>b>0)的一个顶点为A(2,0)，离心率为
.直线y＝k(x－1)与椭圆C交于不同的两点M，N.(1)求椭圆C的方程；
(2)当△AMN的面积为
时，求k的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知圆M过C(1,-1),D(-1,1)两点，且圆心M在x+y-2=0上．
（1）求圆M的方程；
（2）设点P是直线3x+4y+8=0上的动点，PA,PB是圆M的两条切线，A,B为切点，求四边形PAMB面积的最小值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如今,中国的“双十一”已经从一个节日变成了全民狂欢的“电商购物日”.某淘宝电商分析近8年“双十一”期间的宣传费用
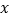(单位:万元)和利润
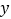(单位:十万元)之间的关系,得到下列数据: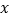2
3
4
5
6
8
9
11
1
2
3
3
4
5
6
8
请回答:
（Ⅰ）请用相关系数
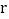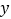说明与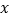之间是否存在线性相关关系(当
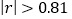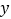时,说明与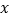之间具有线性相关关系);（Ⅱ）根据1的判断结果,建立
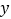与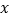之间的回归方程,并预测当
时,对应的利润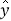
为多少(
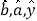精确到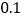
).附参考公式:回归方程中
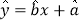中
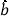和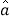
最小二乘估计分别为
,
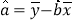,相关系数
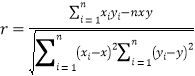.参考数据:
. -
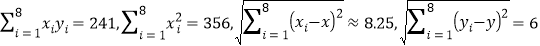科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系xOy中，以原点O为极点，x轴的正半轴为极轴，建立极坐标系，曲线C1的参数方程为
（θ为参数），曲线 C2的极坐标方程为ρcosθ﹣ 
ρsinθ﹣4=0．
（1）求曲线C1的普通方程和曲线 C2的直角坐标方程；
（2）设P为曲线C1上一点，Q为曲线 C2上一点，求|PQ|的最小值． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数f（x）=m﹣|x﹣2|，m∈R，且f（x+2）≥0的解集为[﹣1，1]．
（1）求m的值；
（2）若a，b，c∈R，且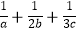
=m，求证：a+2b+3c≥9． -
科目： 来源： 题型：
查看答案和解析>>【题目】下列说法正确的是（ ）
A.命题“x∈R，ex＞0”的否定是“x∈R，ex＞0”
B.命题“已知x，y∈R，若x+y≠3，则x≠2或y≠1”是真命题
C.“x2+2x≥ax在x∈[1，2]上恒成立”“（x2+2x）min≥（ax）max在x∈[1，2]上恒成立”
D.命题“若a=﹣1，则函数f（x）=ax2+2x﹣1只有一个零点”的逆命题为真命题
相关试题
